1. Тип 22 № 7887 

Классификатор алгебры: 1\.5\. Преобразования буквенных выражений со степенями и корнями
Преобразование алгебраических выражений. Задания для подготовки
i
Упростите выражение 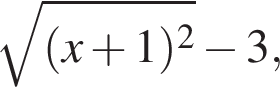 при
при 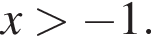
1) 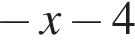
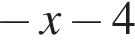
2) 
3) 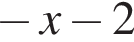
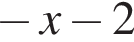
4) 
Решение. Заметим, что  . Поскольку
. Поскольку  то модуль раскроется со знаком плюс. Упростим исходное выражение:
то модуль раскроется со знаком плюс. Упростим исходное выражение:
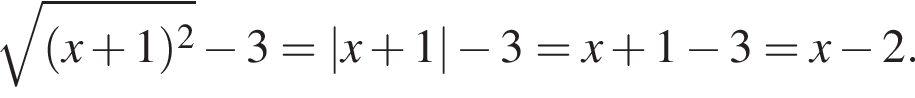
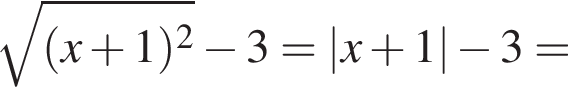
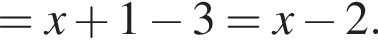
Правильный ответ указан под номером 2.
Ответ: 2
7887
2
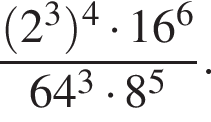
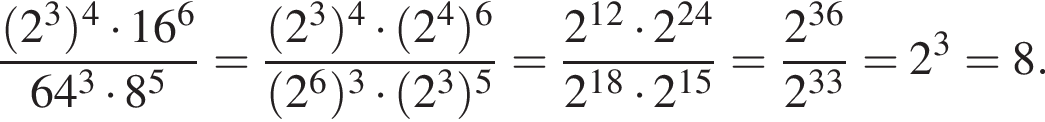
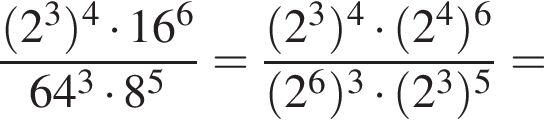
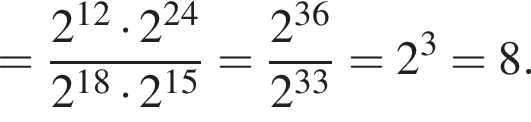
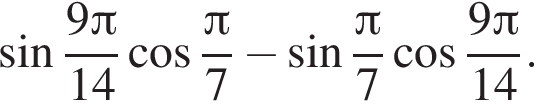
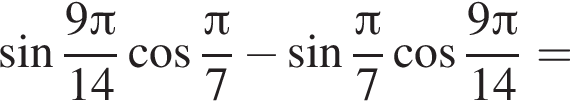
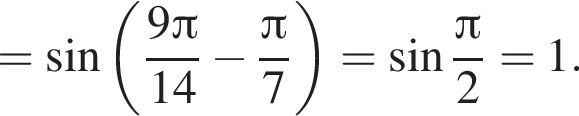
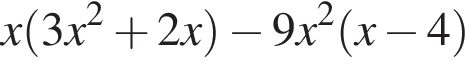
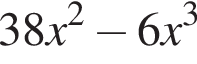
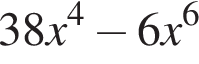
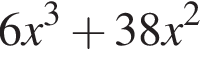
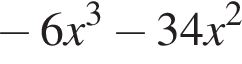
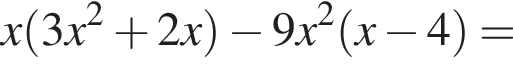
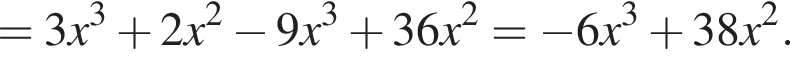
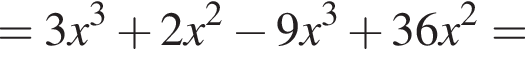
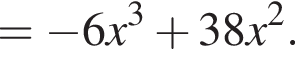

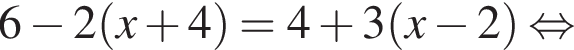
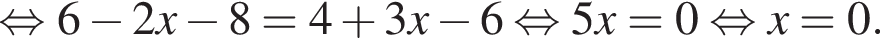

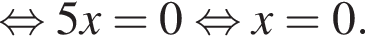
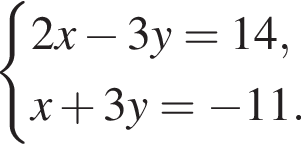
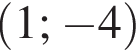
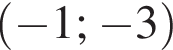
 откуда
откуда 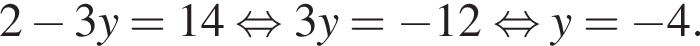
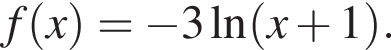
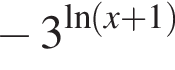
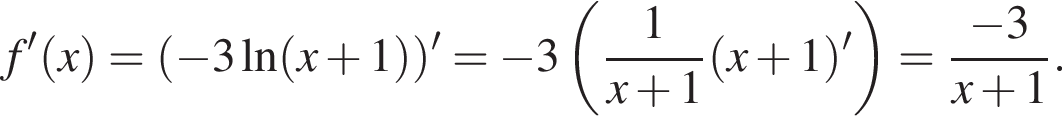
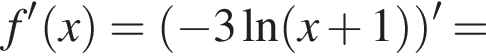
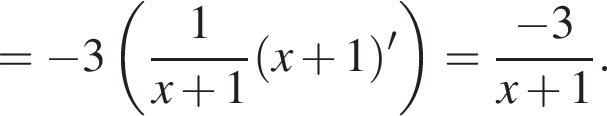
 откуда
откуда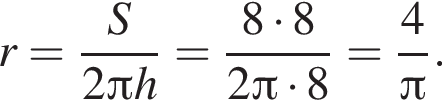
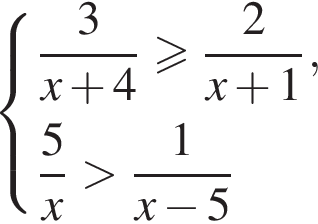 равно
равно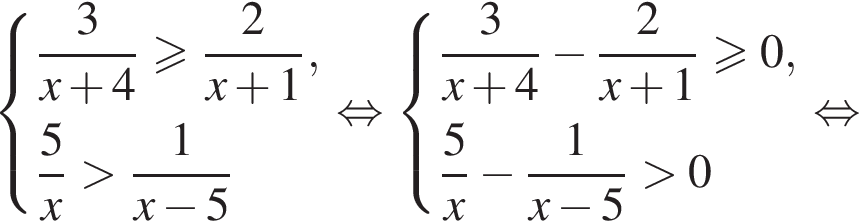
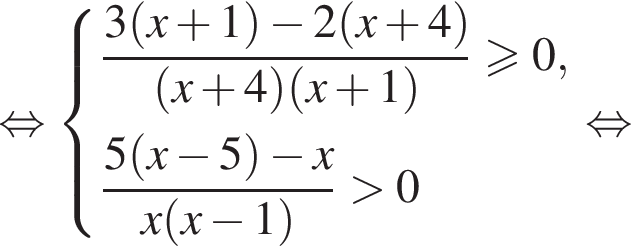
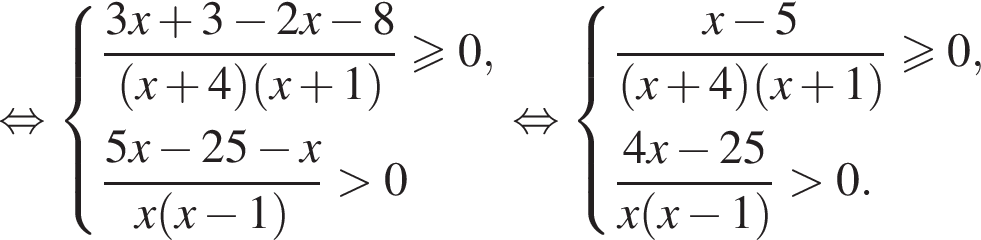
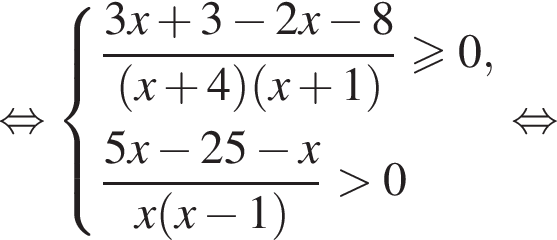
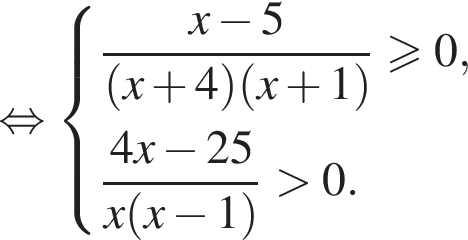
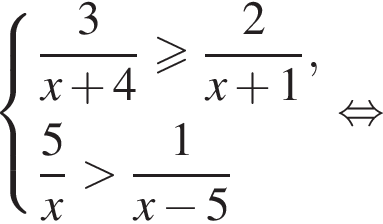
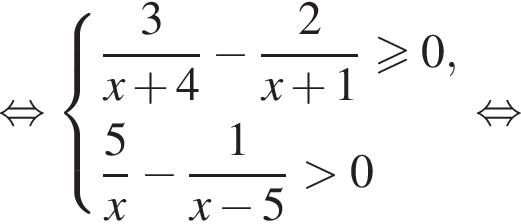
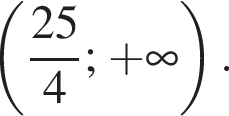 Наименьшее натуральное решение системы неравенств равно 7.
Наименьшее натуральное решение системы неравенств равно 7.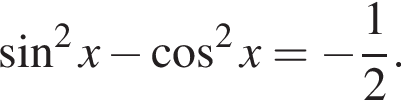
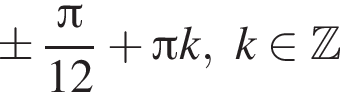
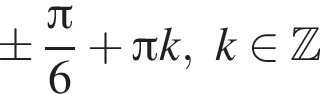
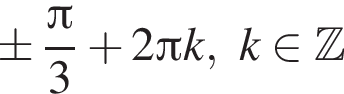
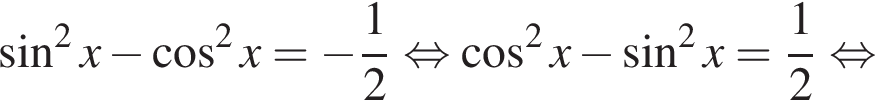
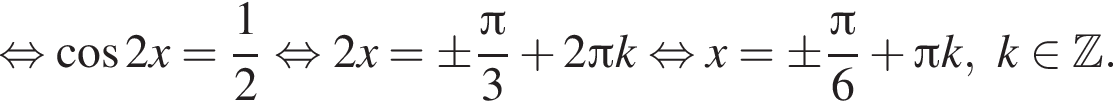
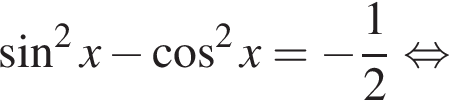
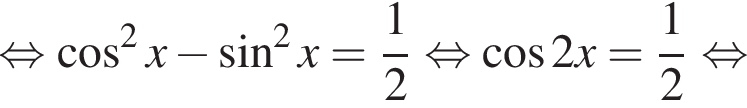
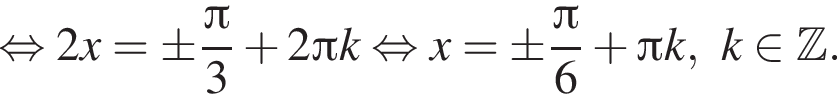
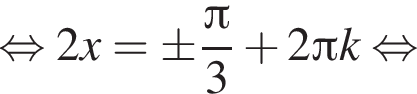
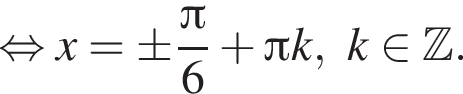
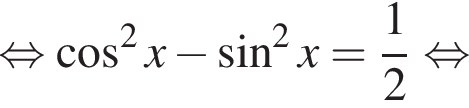
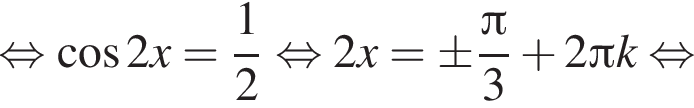
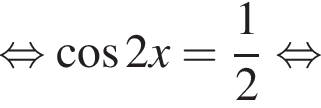
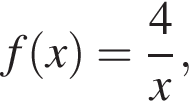 при
при 

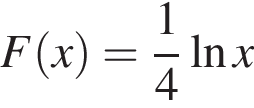
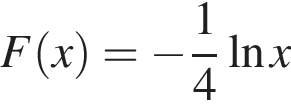
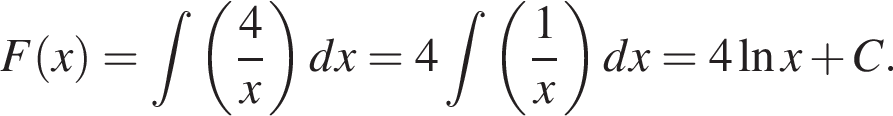
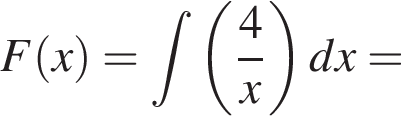
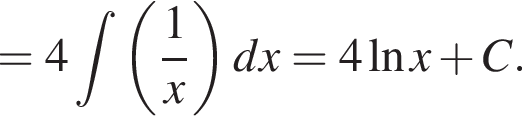
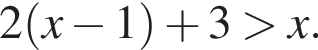

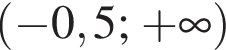

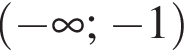
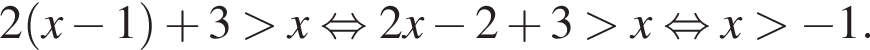


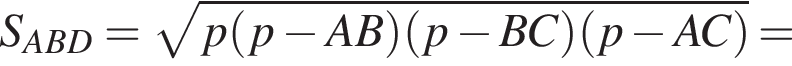
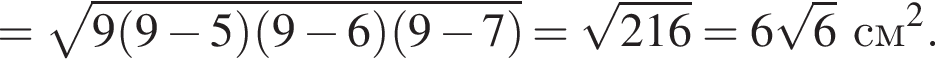
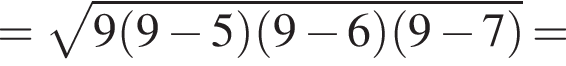
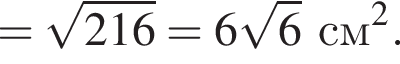
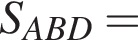
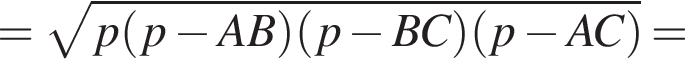
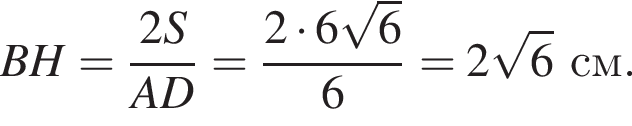
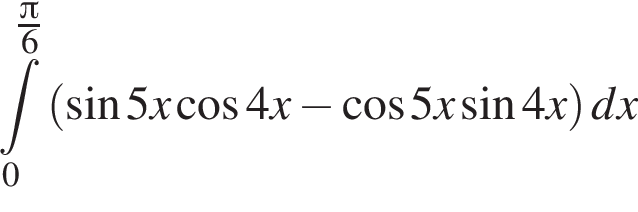
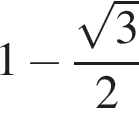
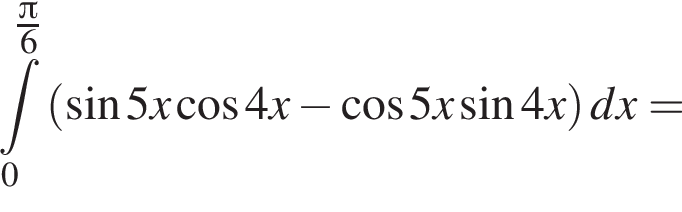
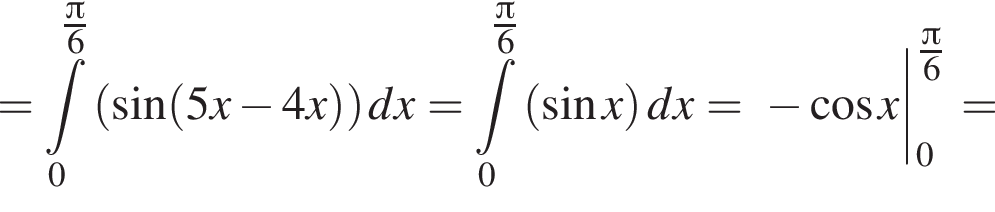
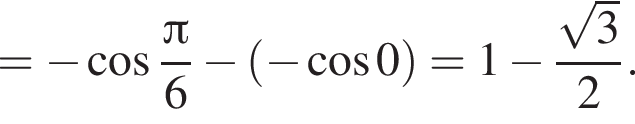
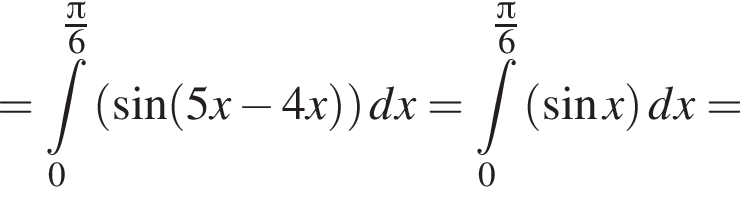
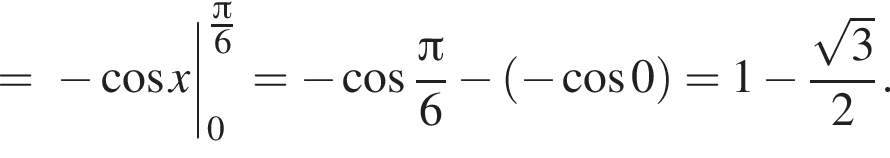
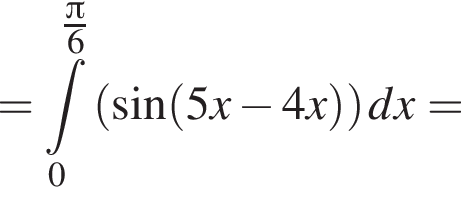
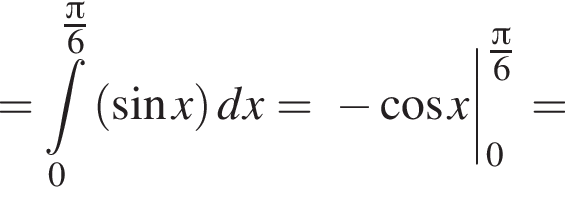
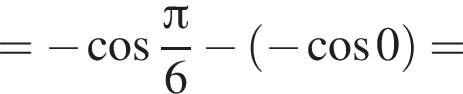
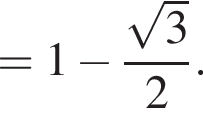
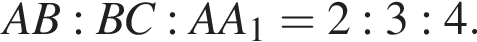

 и
и  Поскольку противоположные ребра в параллелепипеде равны, то
Поскольку противоположные ребра в параллелепипеде равны, то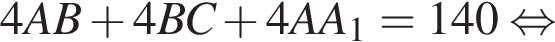
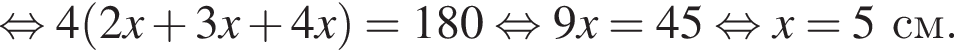


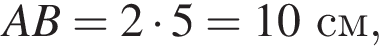

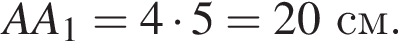
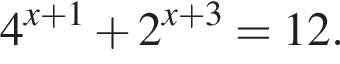
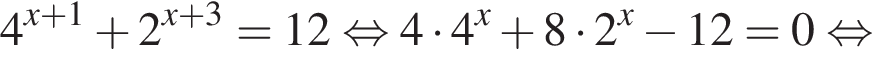
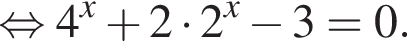
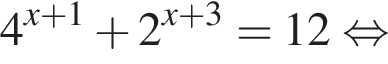
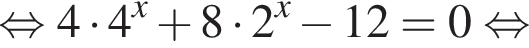
 тогда
тогда
 откуда
откуда 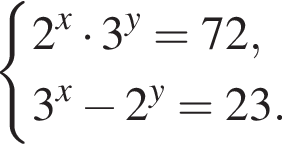
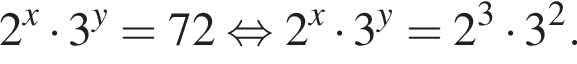
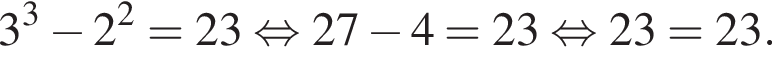
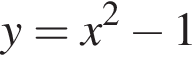 и
и 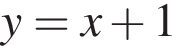 равна
равна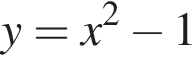 и
и  его корни
его корни 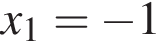 и
и  Для вычисления площади фигуры воспользуемся формулой
Для вычисления площади фигуры воспользуемся формулой 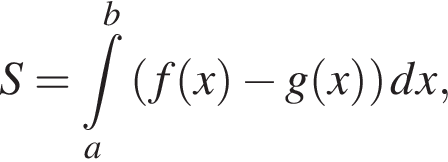 где
где  для
для 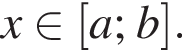 Тогда
Тогда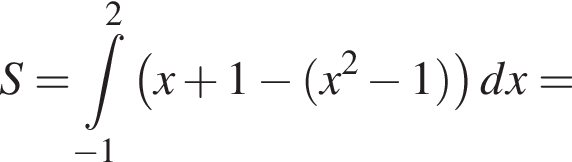
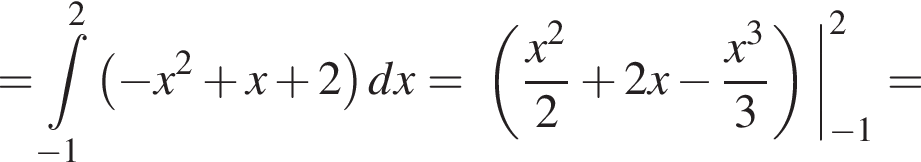
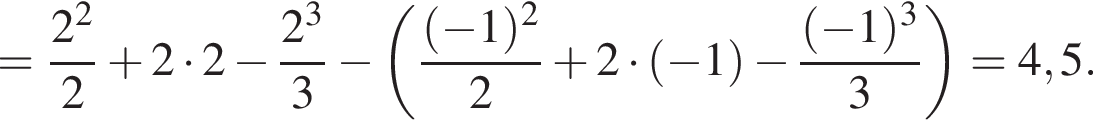
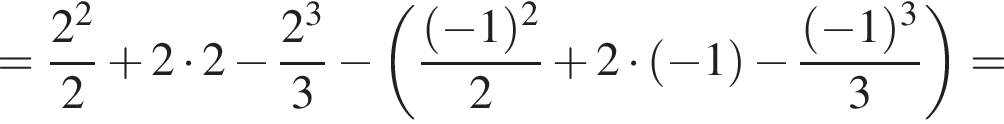
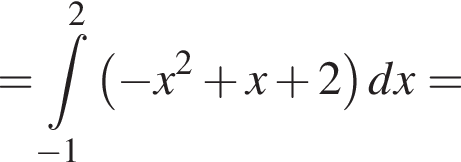
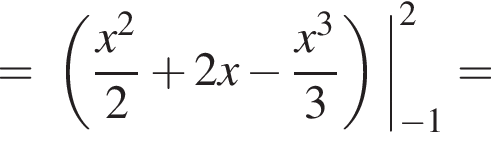
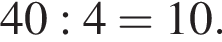 Пусть О — точка пересечения диагоналей ромба. Отрезок AO равен
Пусть О — точка пересечения диагоналей ромба. Отрезок AO равен 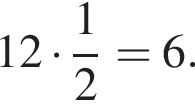 В прямоугольном треугольнике AOB по теореме Пифагора найдем:
В прямоугольном треугольнике AOB по теореме Пифагора найдем: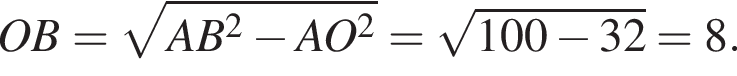
 запишем:
запишем: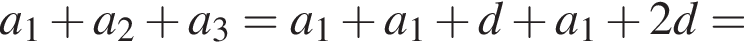
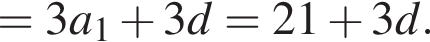
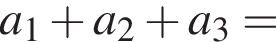
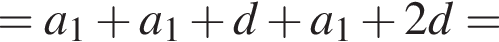



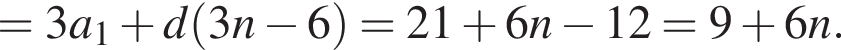
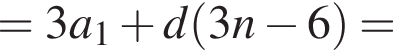
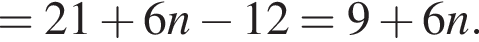

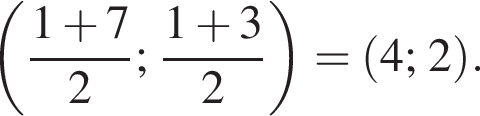
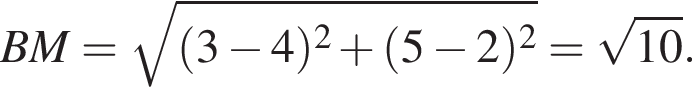
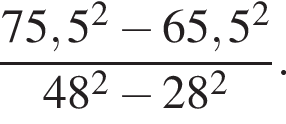
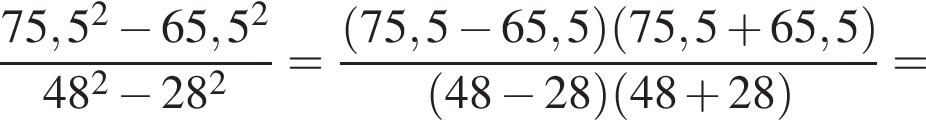
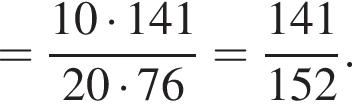
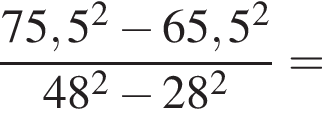
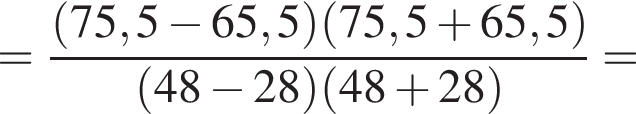
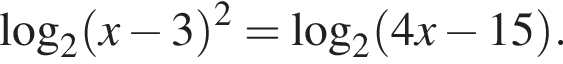
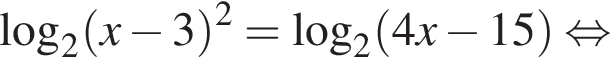
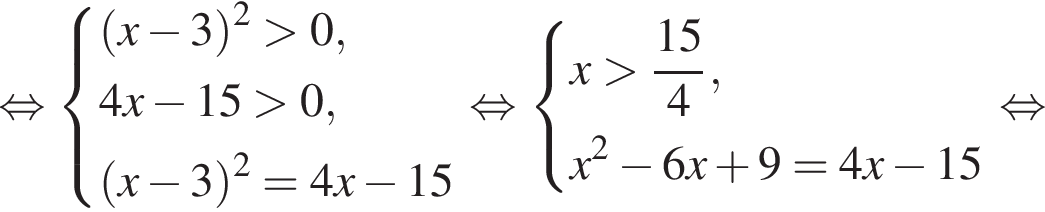
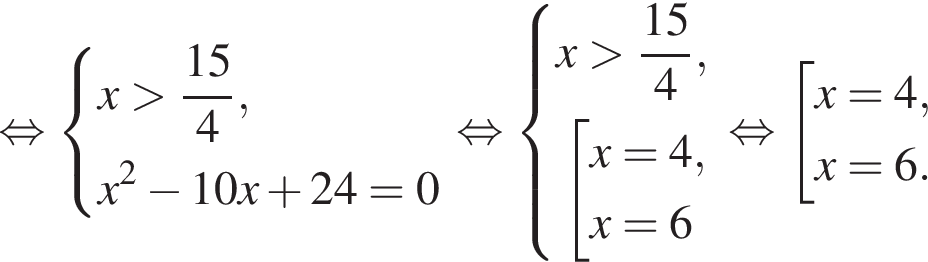
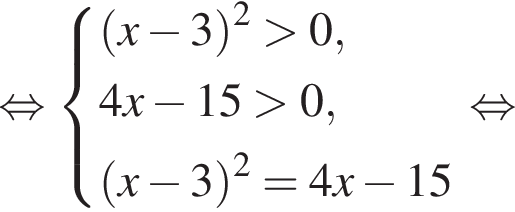
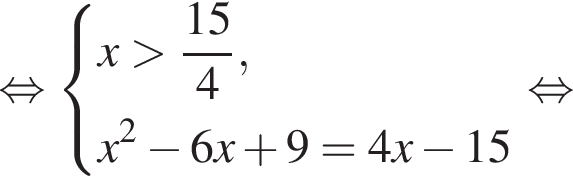
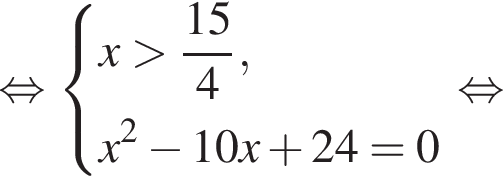
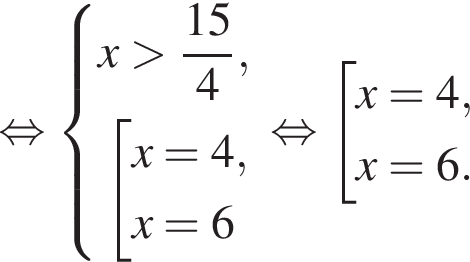
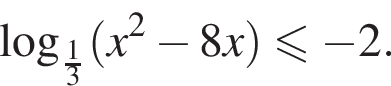

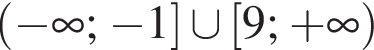

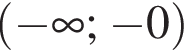

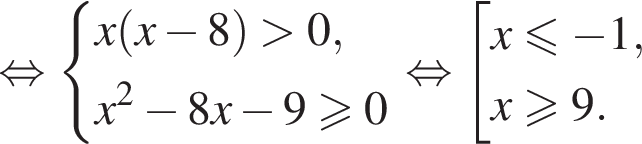
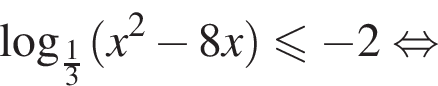
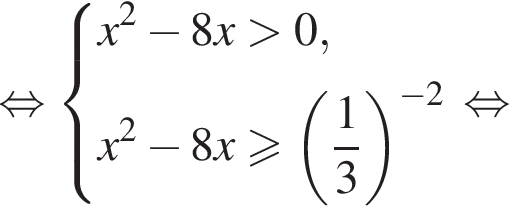
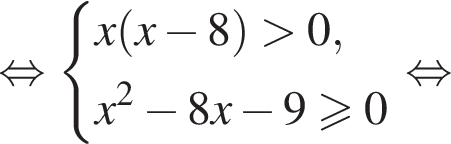
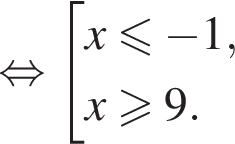
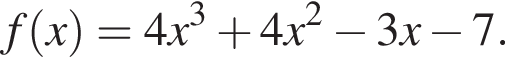
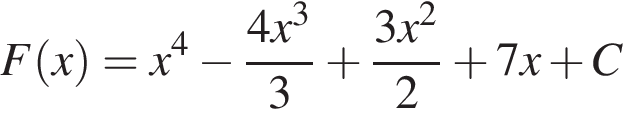
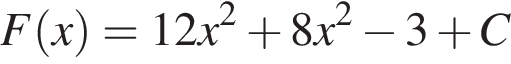
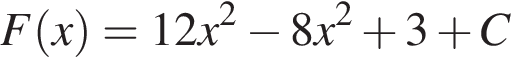
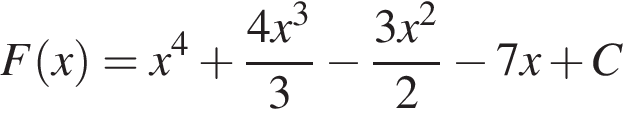
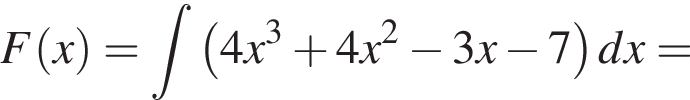
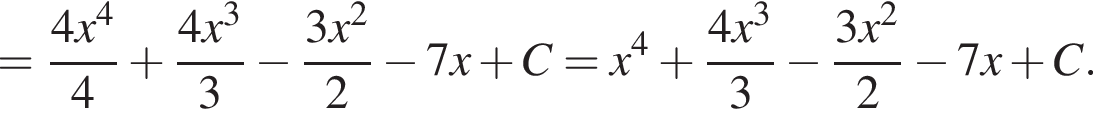
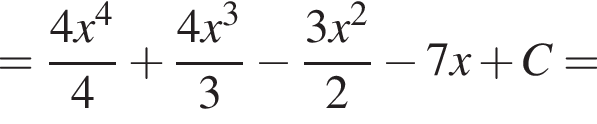
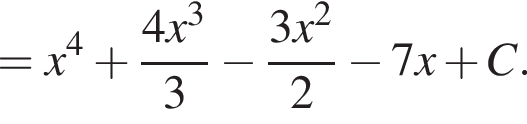

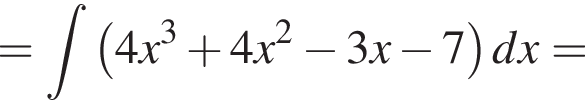
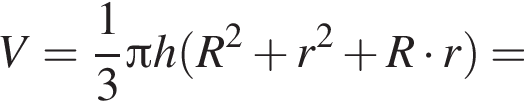
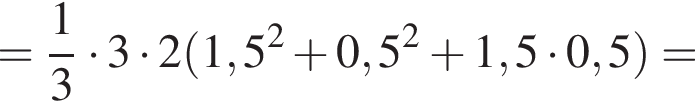
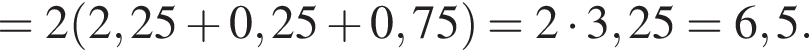
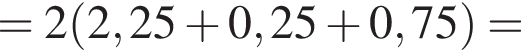

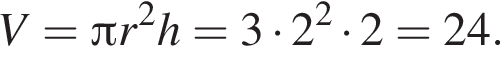
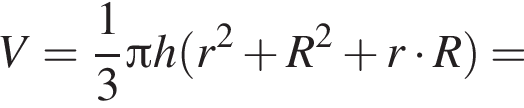
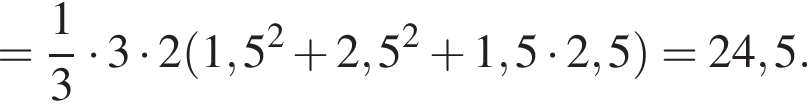
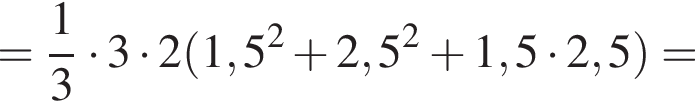
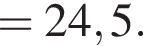
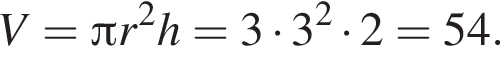

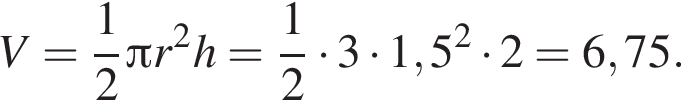
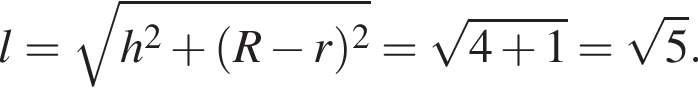

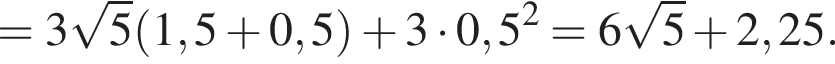
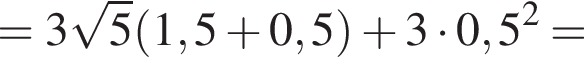
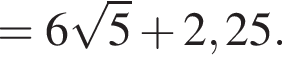
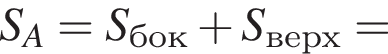
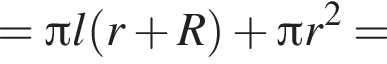


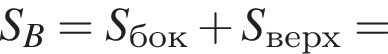
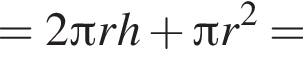
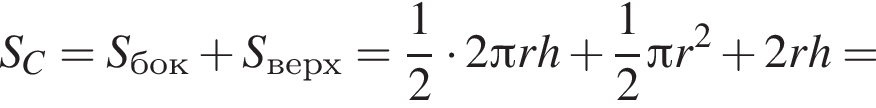
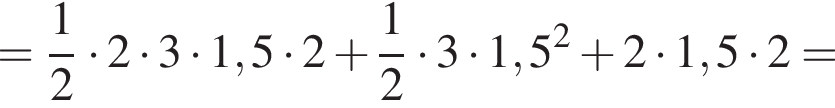

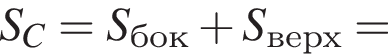
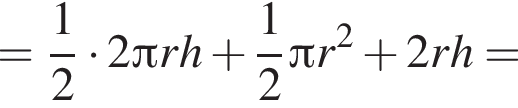


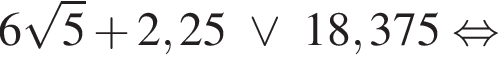
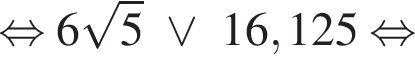

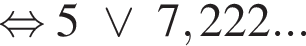
 Установите соответствие между наибольшим и наименьшим значением функции и его числовым значением.
Установите соответствие между наибольшим и наименьшим значением функции и его числовым значением.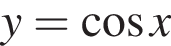 — [−1; 1]. Тогда область допустимых значений функции
— [−1; 1]. Тогда область допустимых значений функции 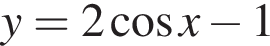 — [−3; 1]. Наибольшее значение функции равно 1, наименьшее значение функции равно −3.
— [−3; 1]. Наибольшее значение функции равно 1, наименьшее значение функции равно −3.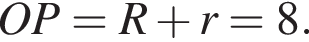
 Только один вариант ответа входит в этот интервал — OP = 7.
Только один вариант ответа входит в этот интервал — OP = 7. Установите соответствие между коэффициентом при x в первой степени и суммой коэффициентов многочлена и промежутком, на котором они верны.
Установите соответствие между коэффициентом при x в первой степени и суммой коэффициентов многочлена и промежутком, на котором они верны.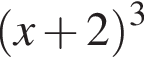 в виде многочлена, используя формулу куба суммы. Имеем:
в виде многочлена, используя формулу куба суммы. Имеем: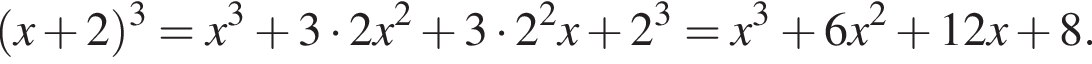
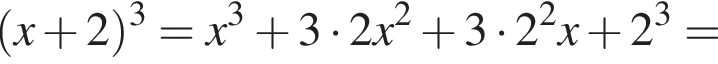
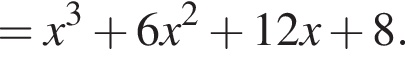
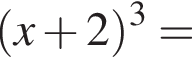

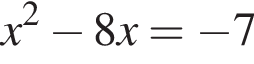 и
и 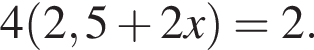 По представленным данным установите соответствие.
По представленным данным установите соответствие.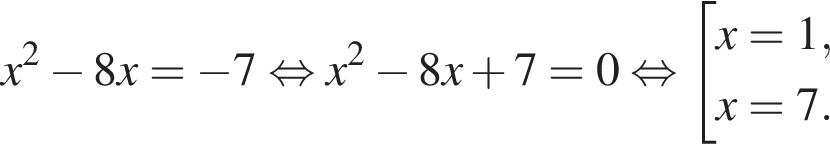
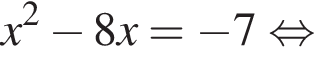
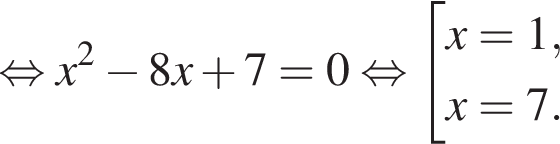
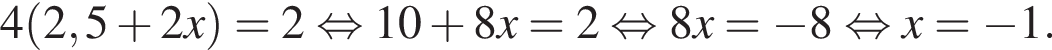

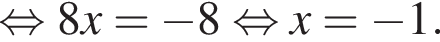
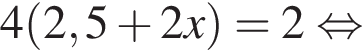
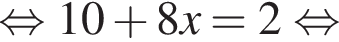
 Установите соответствие между выражением и его числовым значением.
Установите соответствие между выражением и его числовым значением.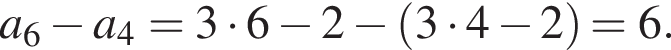
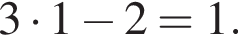 Найдем сумму первых пяти членов прогрессии:
Найдем сумму первых пяти членов прогрессии: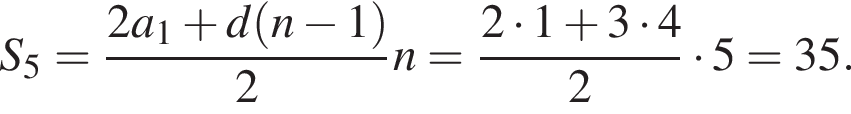
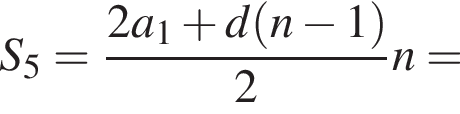
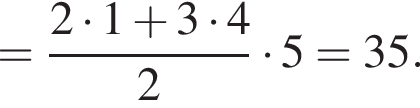








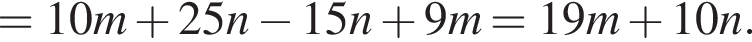
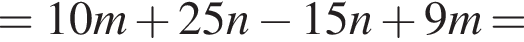
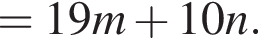
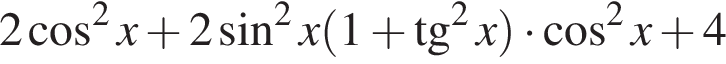 равно
равно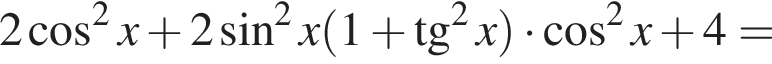
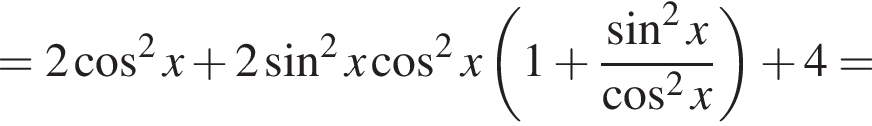
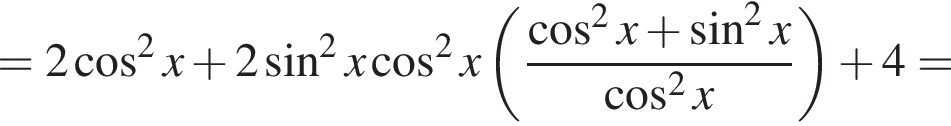
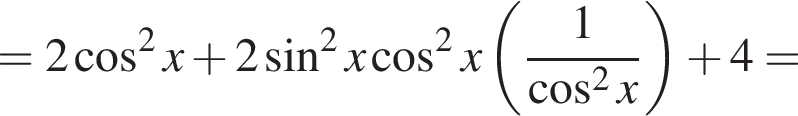

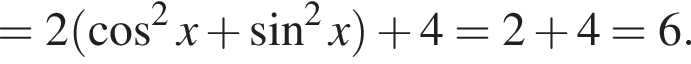
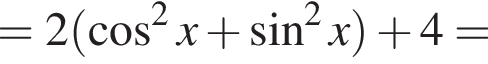
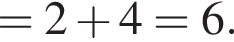
 то вычислите сумму первого члена и разности этой прогрессии
то вычислите сумму первого члена и разности этой прогрессии откуда
откуда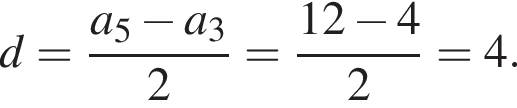
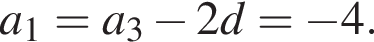 Следовательно, сумма первого члена и разности данной прогрессии равна 0.
Следовательно, сумма первого члена и разности данной прогрессии равна 0.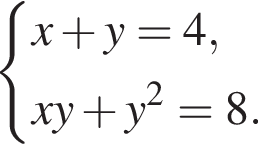

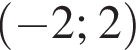
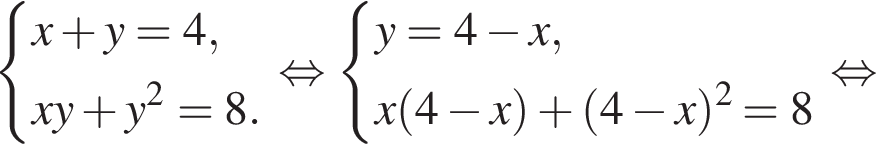
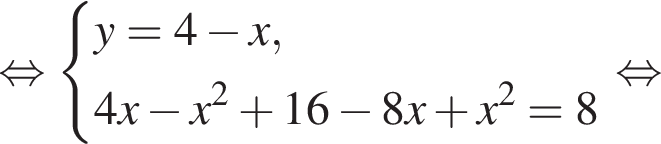
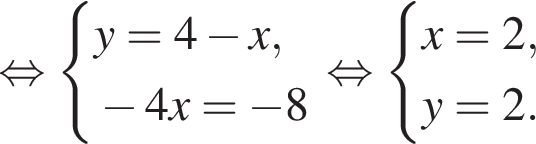
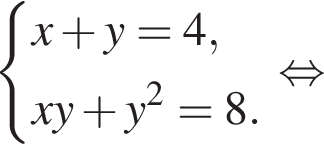
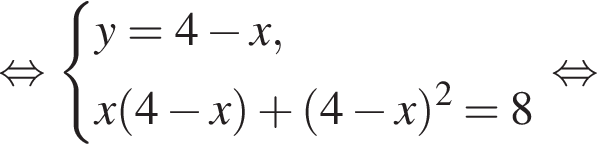
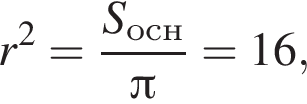 откуда
откуда