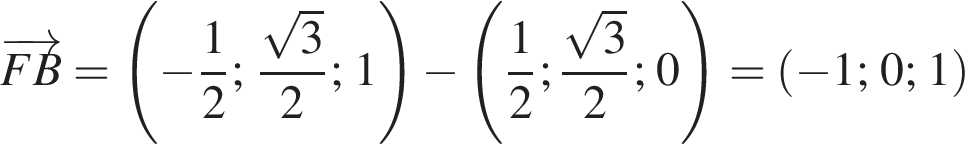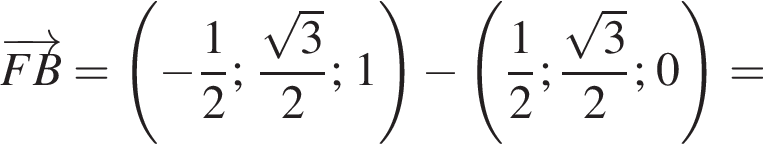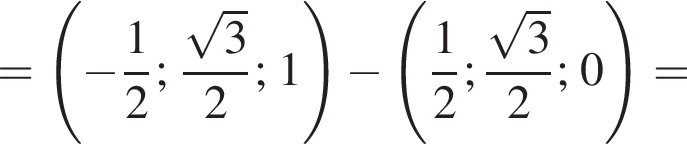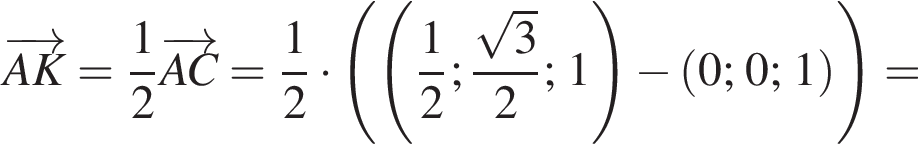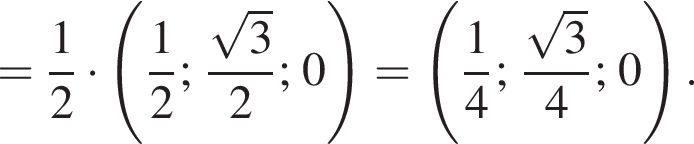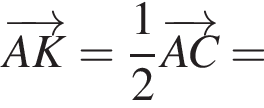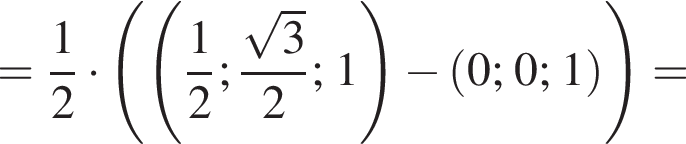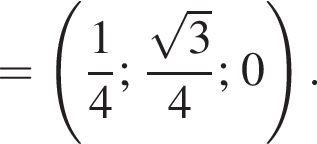Приведите одночлен 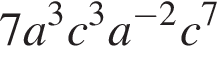 к стандартному виду.
к стандартному виду.
1) 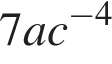
2) 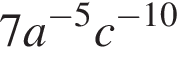
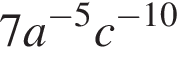
3) 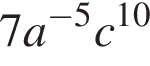
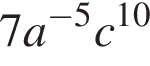
4) 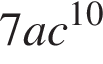
5) 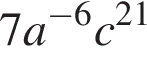
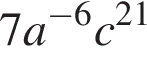
Решение. Преобразуем исходное выражение:



Правильный ответ указан под номером 4.
Примечание Решу ЕНТ.
Обращаем внимание читателя, что выражение 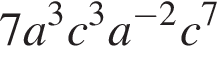 не является одночленом, поскольку содержит отрицательную степень одного из множителей.
не является одночленом, поскольку содержит отрицательную степень одного из множителей.
Ответ: 4
606
4
Источники:

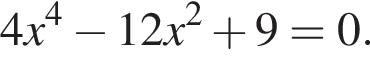

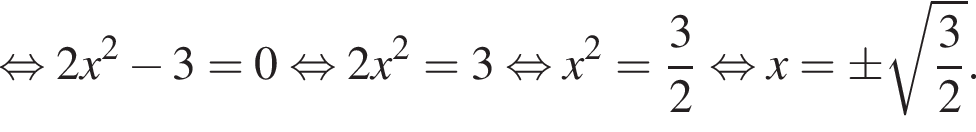
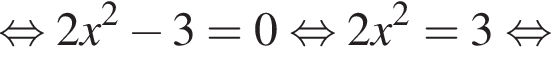
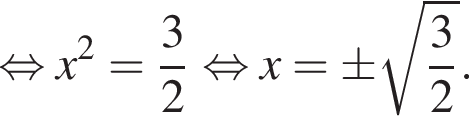
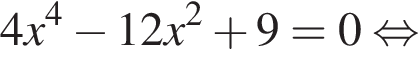
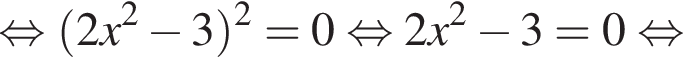

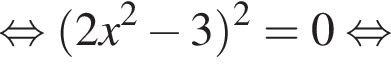
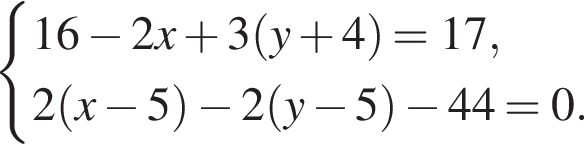
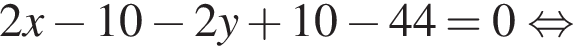

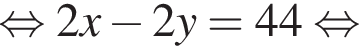
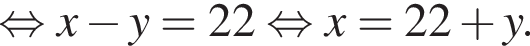
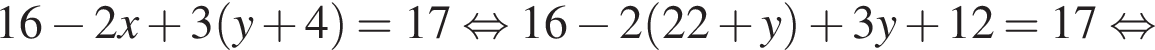
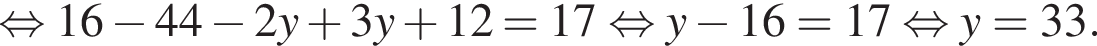
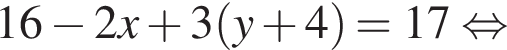
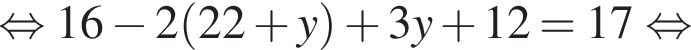

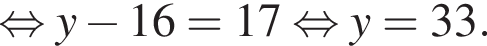
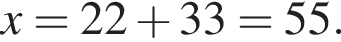
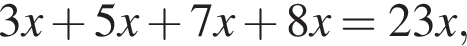 при этом
при этом  откуда
откуда 

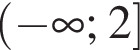
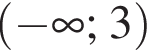



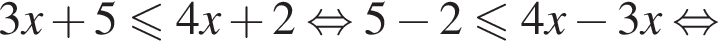

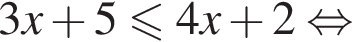

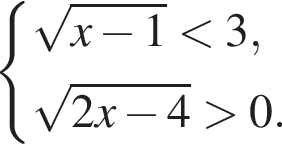
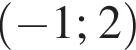
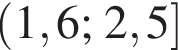
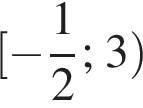
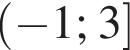

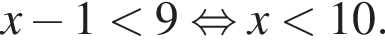
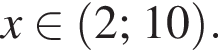
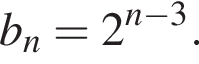
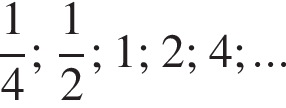
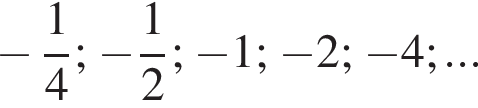
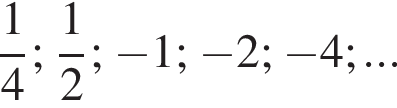
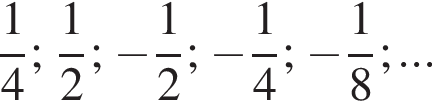
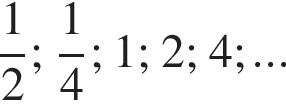

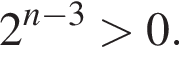 Эти два соображения оставляют возможным только первый ответ и он действительно подходит при всех
Эти два соображения оставляют возможным только первый ответ и он действительно подходит при всех 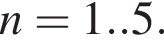
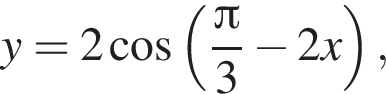 найдите
найдите 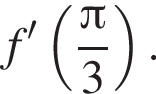
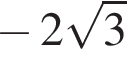
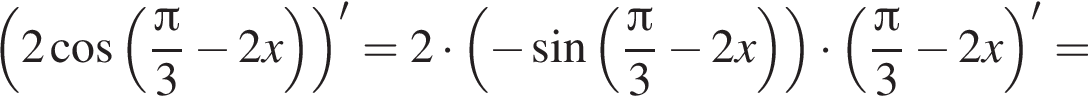
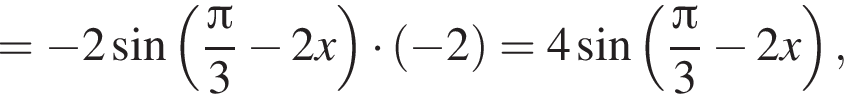
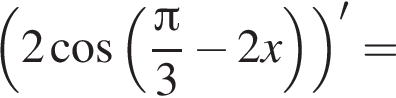
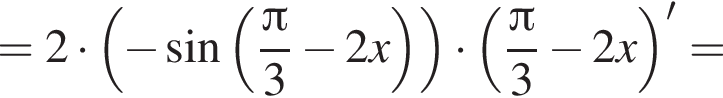
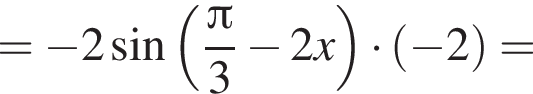
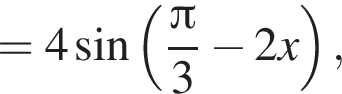

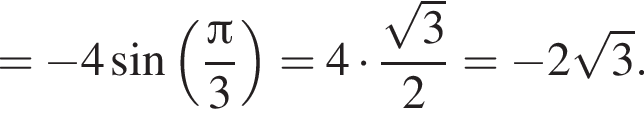
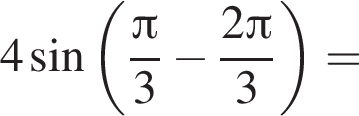
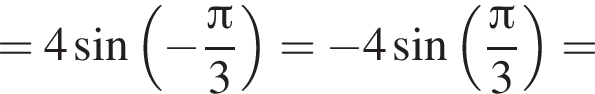
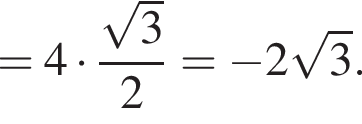
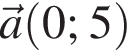 и
и 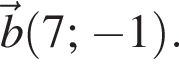 Косинус угла между векторами
Косинус угла между векторами  и
и 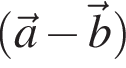 равен?
равен?
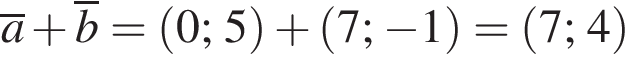
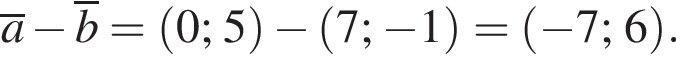
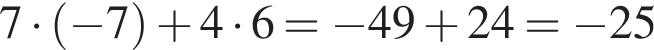
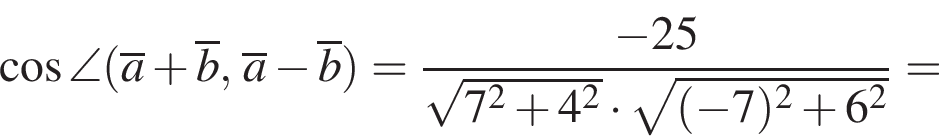
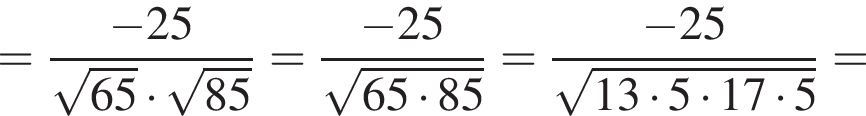

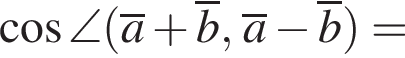
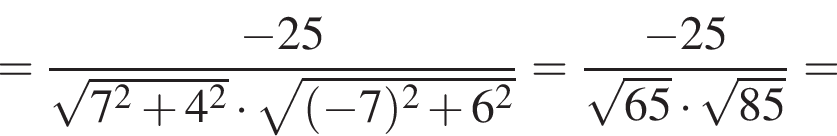
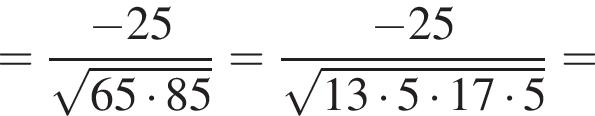
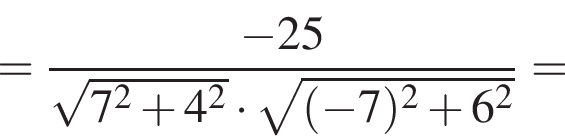
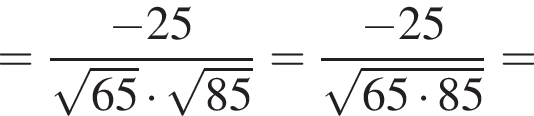
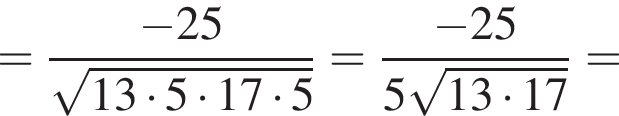
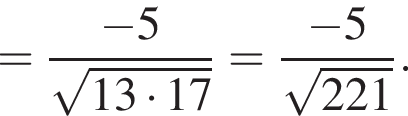
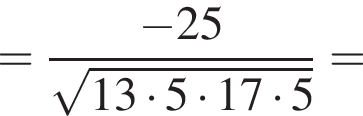
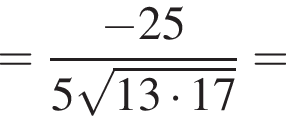
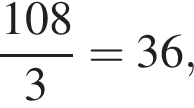 откуда и высота призмы, и сторона ее основания равны 6. Площадь правильного треугольника со стороной a равна
откуда и высота призмы, и сторона ее основания равны 6. Площадь правильного треугольника со стороной a равна 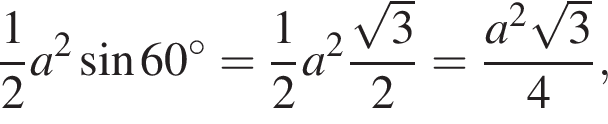

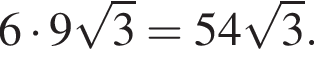
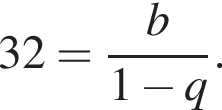
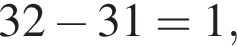 при этом они тоже образуют бесконечно убывающую геометрическую прогрессию. Значит,
при этом они тоже образуют бесконечно убывающую геометрическую прогрессию. Значит, 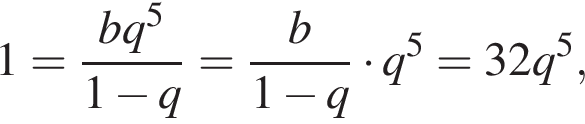
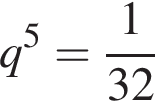 и
и 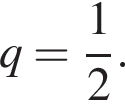 Тогда
Тогда 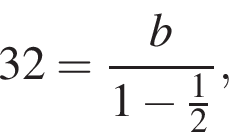 поэтому
поэтому  откуда
откуда 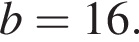
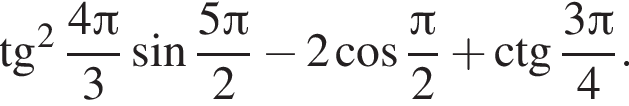
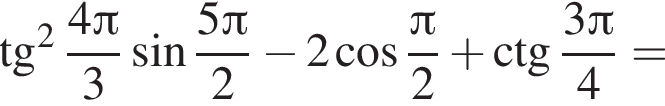
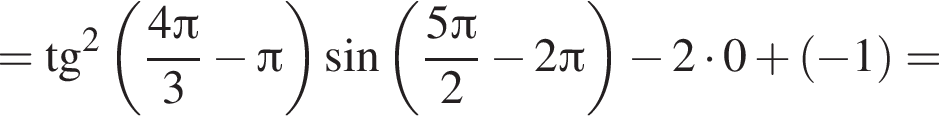
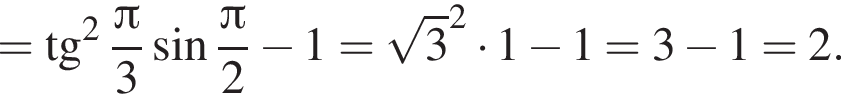

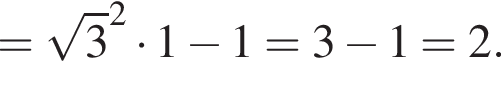
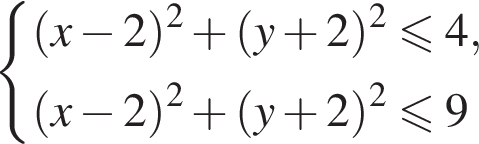
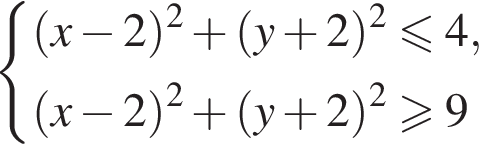
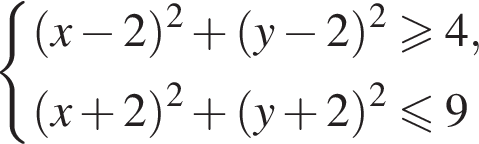
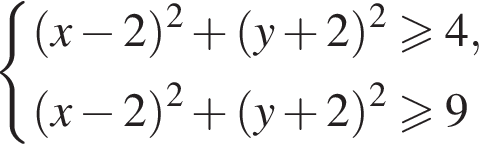
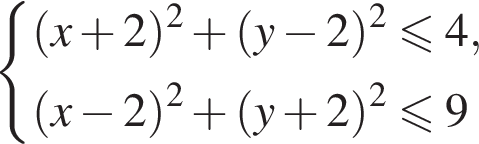
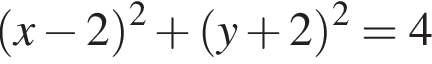 и
и 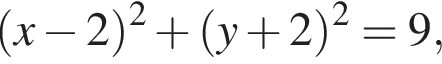 поэтому ответом будет первая система.
поэтому ответом будет первая система.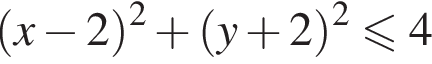 есть еще только во второй системе, но ее второе неравенство задает внешнюю часть круга, поэтому у системы вообще нет решений.
есть еще только во второй системе, но ее второе неравенство задает внешнюю часть круга, поэтому у системы вообще нет решений.


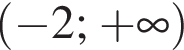
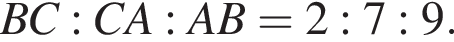 Больший угол треугольника COA равен?
Больший угол треугольника COA равен?


 Поскольку он тупой, он и есть самый большой угол в треугольнике COA
Поскольку он тупой, он и есть самый большой угол в треугольнике COA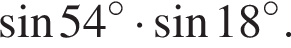
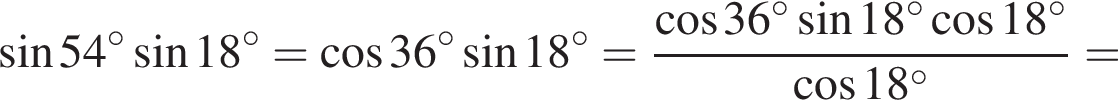
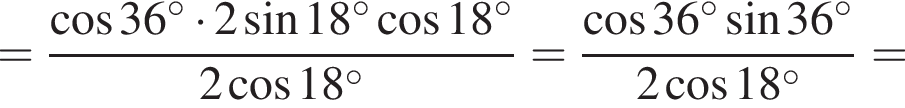
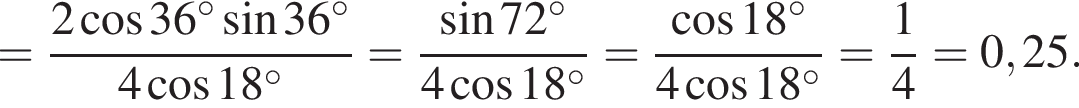
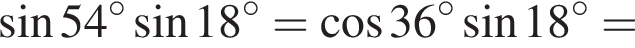
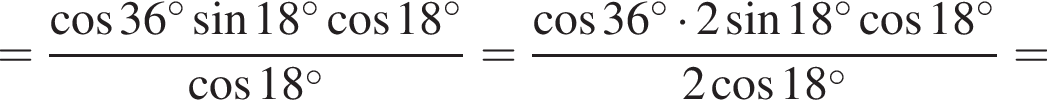
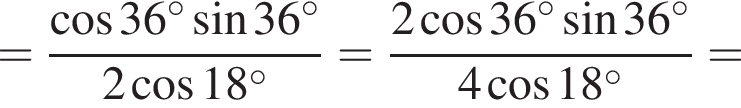
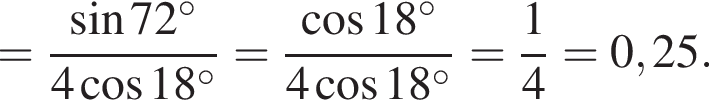
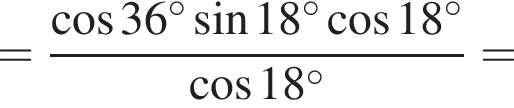
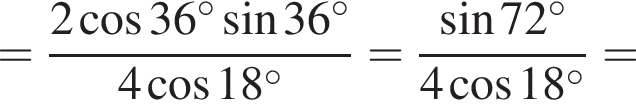
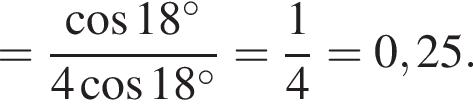
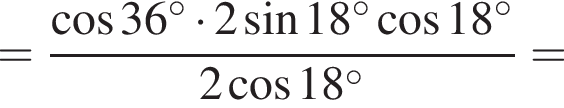
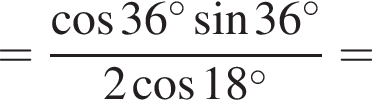


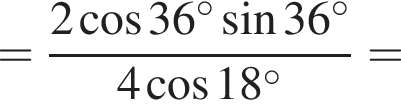
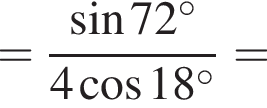
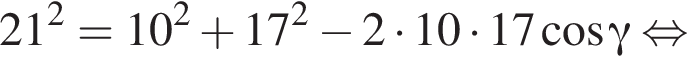

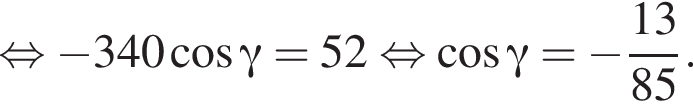

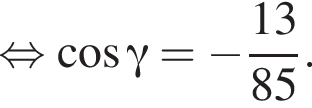

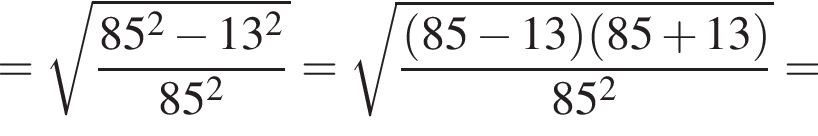
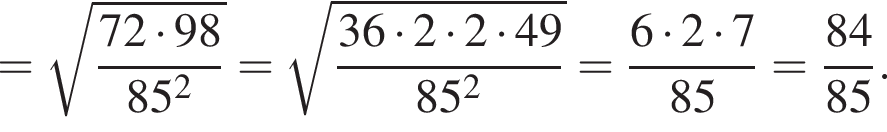
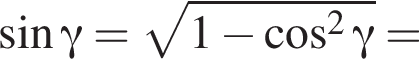
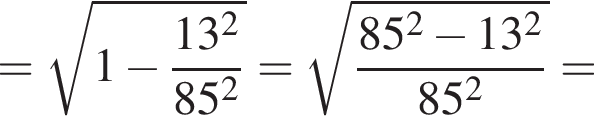
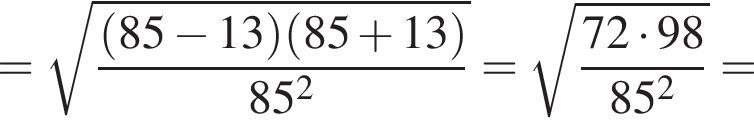
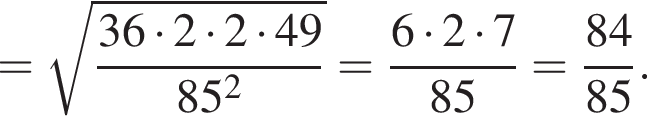
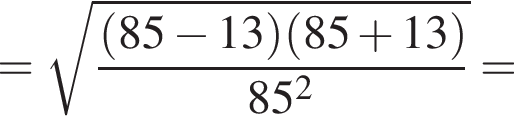
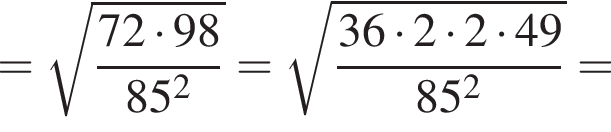
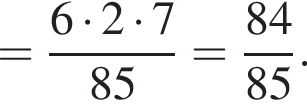
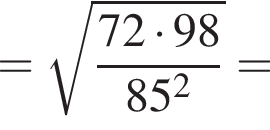

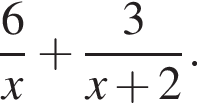 Составим уравнение и решим его.
Составим уравнение и решим его.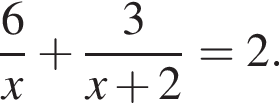



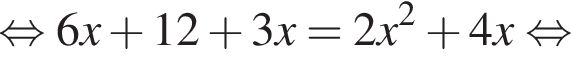
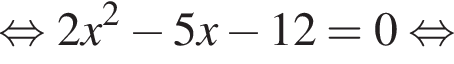
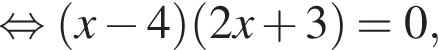
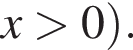 Тогда время для обратного пути (когда все подъемы и спуски поменяются местами) составит
Тогда время для обратного пути (когда все подъемы и спуски поменяются местами) составит 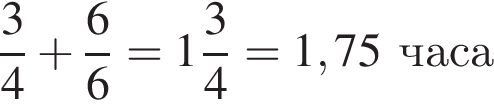
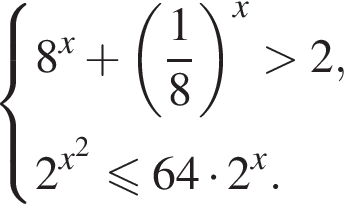
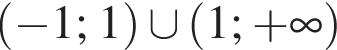
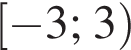
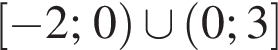

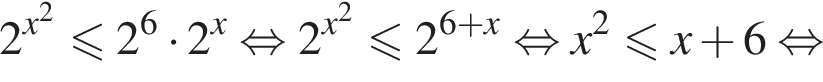
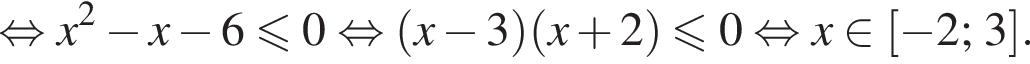
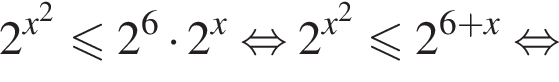
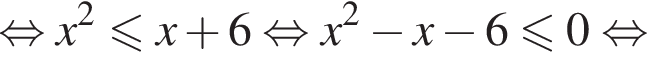

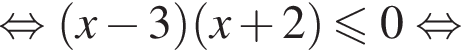
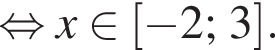

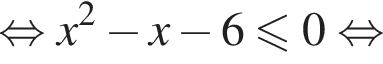
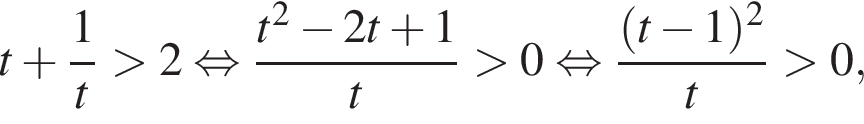
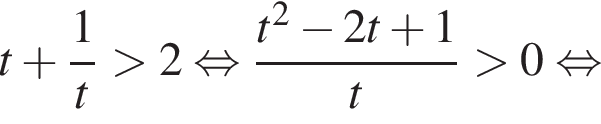
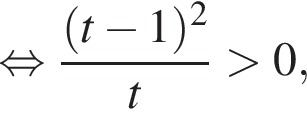
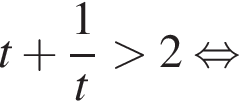

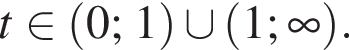 Ясно что
Ясно что  то есть
то есть 
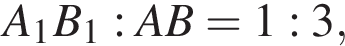 то высоты пирамид SABC и SA1B1C1 различаются также втрое и высота усеченной пирамиды равна
то высоты пирамид SABC и SA1B1C1 различаются также втрое и высота усеченной пирамиды равна 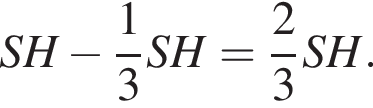 Будем теперь искать SH. Рассмотрим прямоугольный треугольник SHH1, где H1 — середина AC. В нем
Будем теперь искать SH. Рассмотрим прямоугольный треугольник SHH1, где H1 — середина AC. В нем 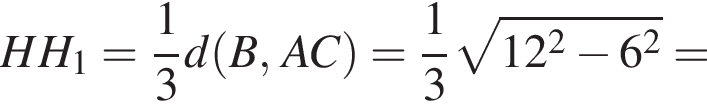
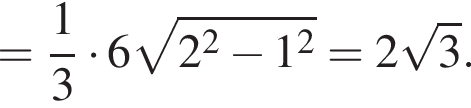

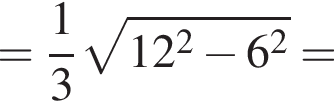
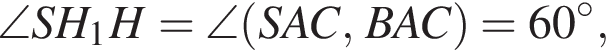
 и
и  Значит,
Значит, 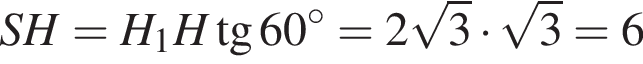
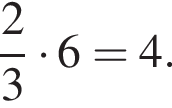
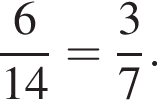
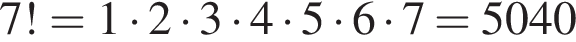
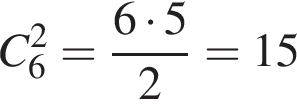 способов выбрать два тела для полки, в каждом из них есть 3 способа выбрать полку. Значит, ответ
способов выбрать два тела для полки, в каждом из них есть 3 способа выбрать полку. Значит, ответ 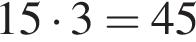 способов.
способов.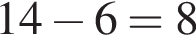 способов выбрать многогранник и 3 способа выбрать полку, что дает
способов выбрать многогранник и 3 способа выбрать полку, что дает 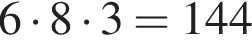 способа.
способа.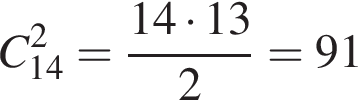 способ выбрать два тела для верхней полки. В
способ выбрать два тела для верхней полки. В 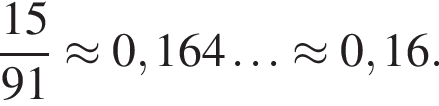
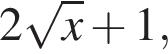

 следовательно,
следовательно,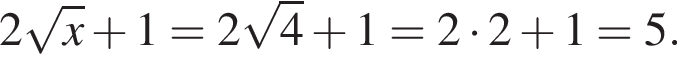
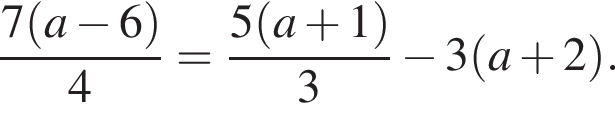
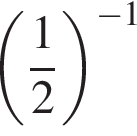
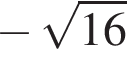
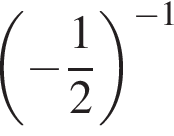
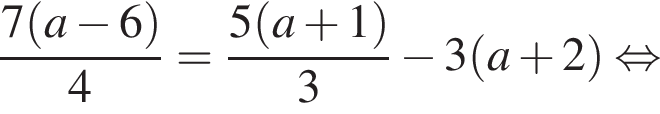
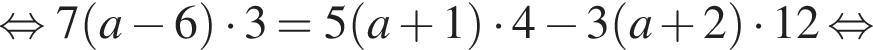
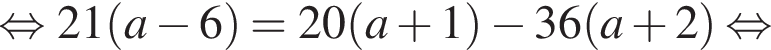
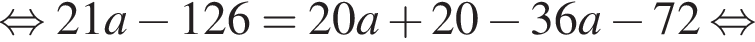

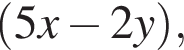 где (x; y) — решение системы уравнений:
где (x; y) — решение системы уравнений: 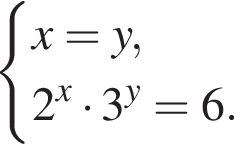


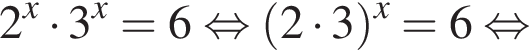
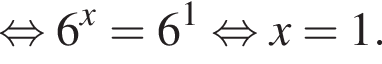
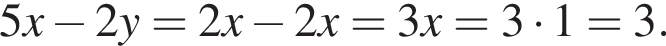
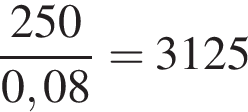 граммов.
граммов.

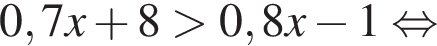
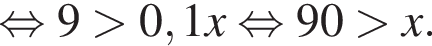
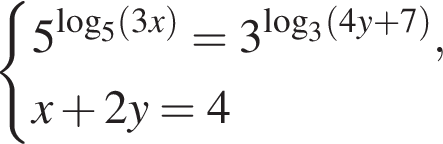
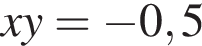

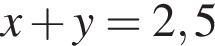

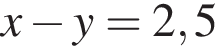

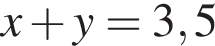
 (при условии, что логарифмы определены). Из второго равнения выразим
(при условии, что логарифмы определены). Из второго равнения выразим 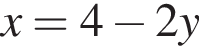 и подставим в новое первое. Получим
и подставим в новое первое. Получим 
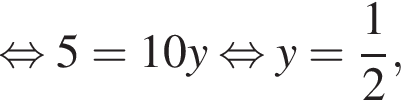


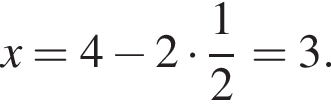 Значит,
Значит, 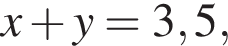
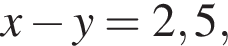
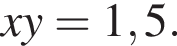
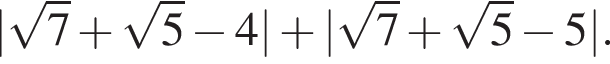
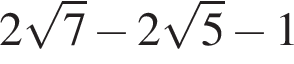
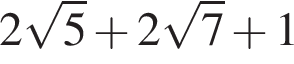
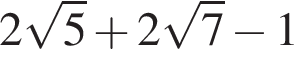
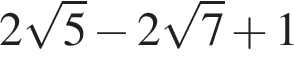
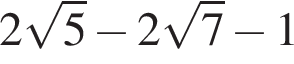
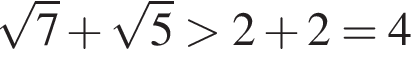 и
и 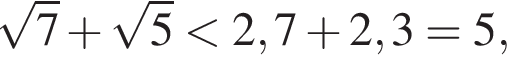 поэтому
поэтому 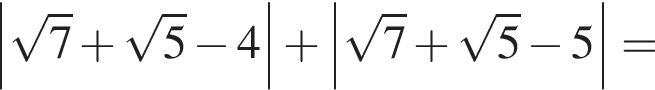
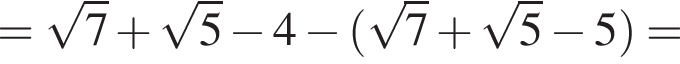
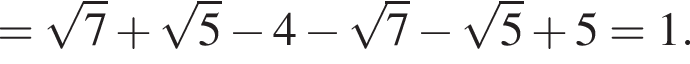

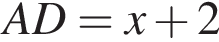 и периметр параллелограмма равен
и периметр параллелограмма равен 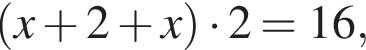 откуда
откуда 
 и по теореме Пифагора
и по теореме Пифагора 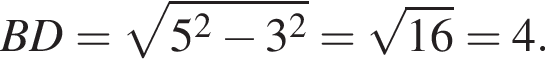
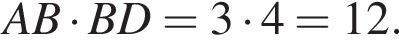
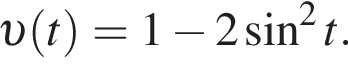 Найдите интервал, в который входит значение пути, пройденного материальной точкой за промежуток времени от
Найдите интервал, в который входит значение пути, пройденного материальной точкой за промежуток времени от 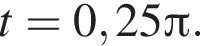
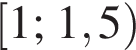
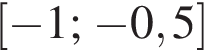
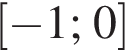


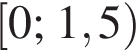
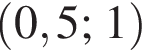
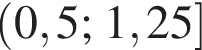
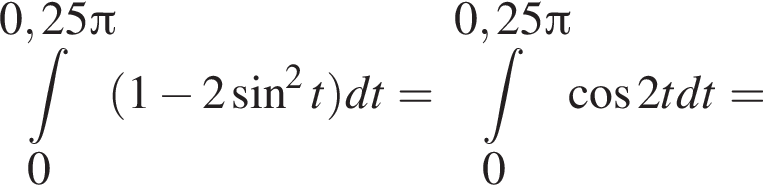
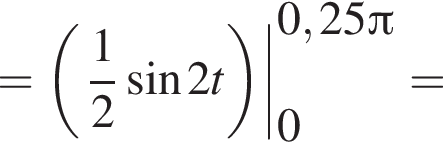
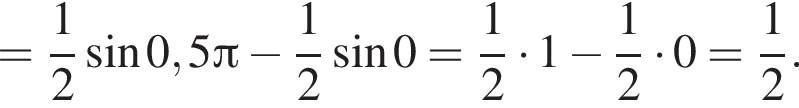
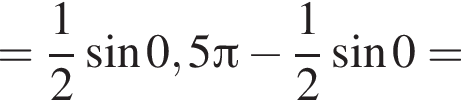
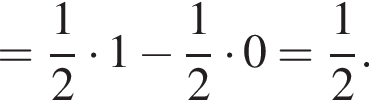
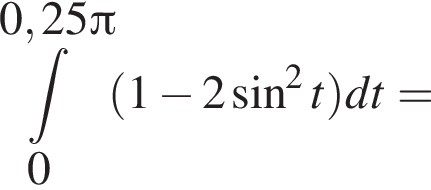
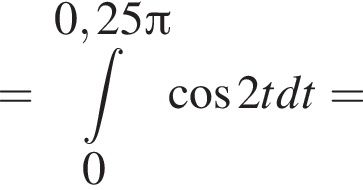
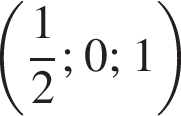
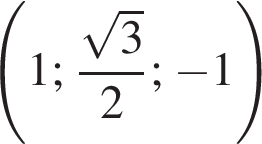
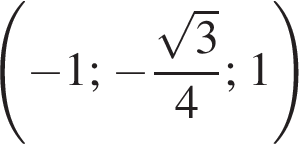
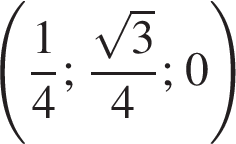
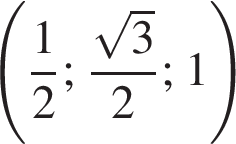
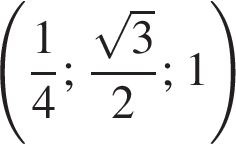
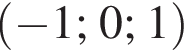
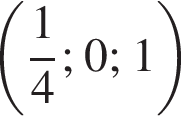
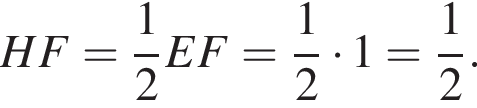
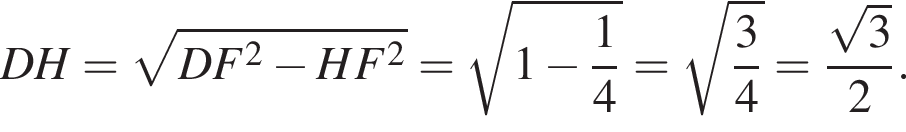

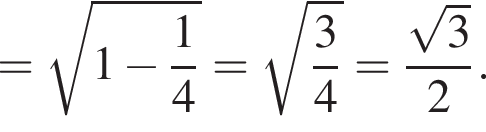
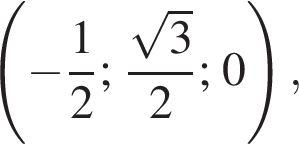 а у точки B, проекция которой на нижнюю плоскость — точка E, координаты будут
а у точки B, проекция которой на нижнюю плоскость — точка E, координаты будут 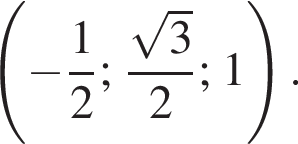 Аналогично у точки C координаты будут
Аналогично у точки C координаты будут 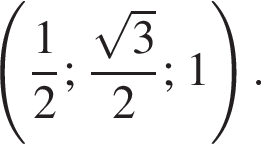 Тогда
Тогда