31. Тип 38 № 3835 
Источник: Реальная версия ЕНТ по математике 2021 года, вариант 2. Отредактировано редакцией Решу ЕНТ в формат актуальной демоверсии
Мультивыбор: прогрессии и последовательности. Задания для подготовки
i
Дана последовательность натуральных чисел, меньших 170, дающих остаток 1 при делении на 19. Выберите верные утверждения.
1) Сумма всех чисел равна 690.
2) Таких чисел 8.
3) Сумма всех чисел равна 695.
4) Разность двух рядом стоящих чисел равна 18.
5) Разность между первым и последним числом равна 150.
6) Сумма всех чисел равна 692.
Решение. Если вычесть из этих чисел по единице, получатся числа, кратные 19, то есть 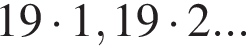 Выпишем эти числа до 149 и сразу прибавим единицу. Получим числа 20, 39, 58, 77, 96, 115, 134, 153 (а число 172 уже слишком велико). Сумма этих восьми чисел составляет
Выпишем эти числа до 149 и сразу прибавим единицу. Получим числа 20, 39, 58, 77, 96, 115, 134, 153 (а число 172 уже слишком велико). Сумма этих восьми чисел составляет
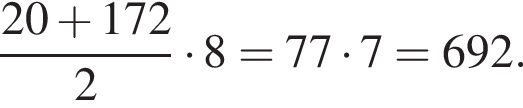
Верны утверждения 2 и 6.
Правильные ответы указаны под номерами 2 и 6.
Ответ: 26
Источник: Реальная версия ЕНТ по математике 2021 года, вариант 2. Отредактировано редакцией Решу ЕНТ в формат актуальной демоверсии


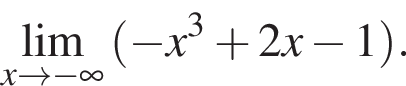
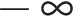

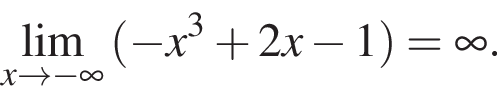


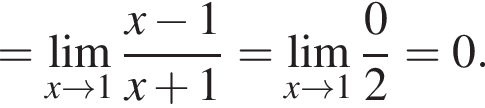
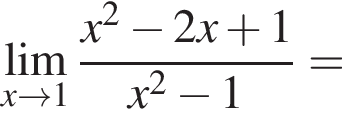

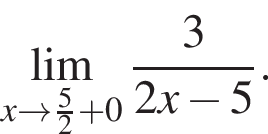
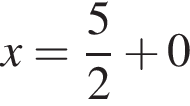 в функцию и находим предел:
в функцию и находим предел:
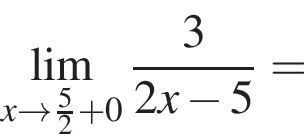
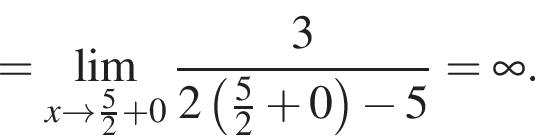
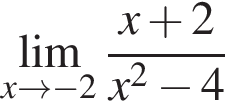
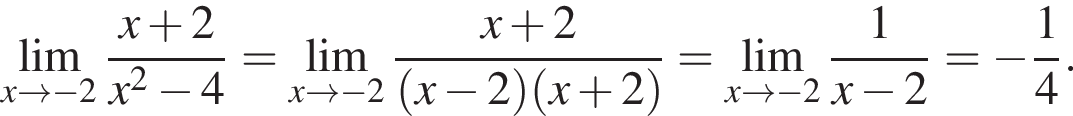
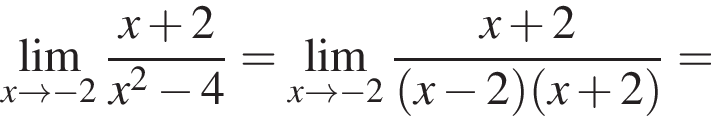
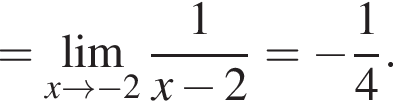
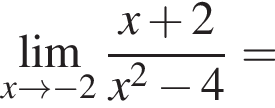
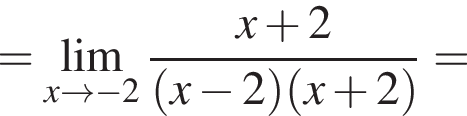
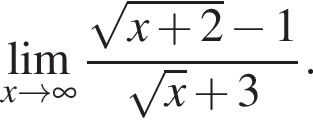
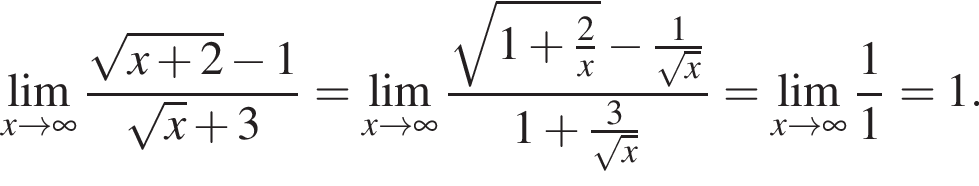
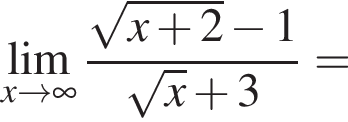
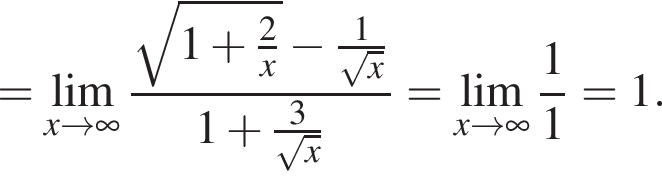
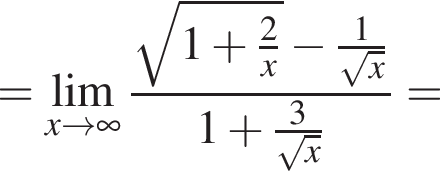
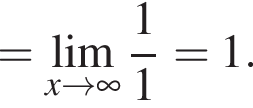
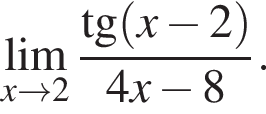
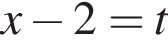 и используем первый замечательный предел.
и используем первый замечательный предел.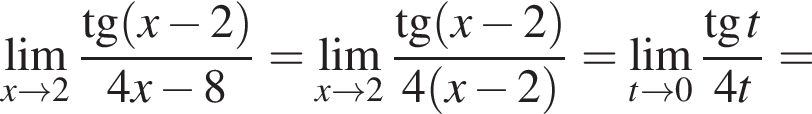
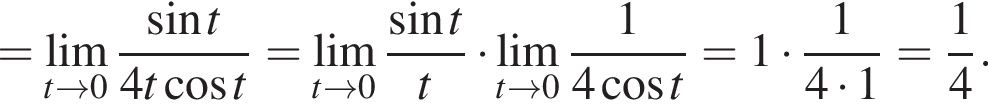
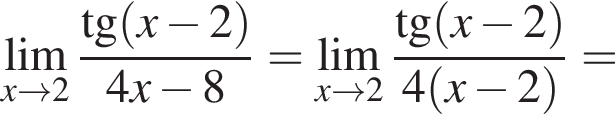
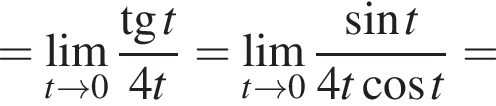
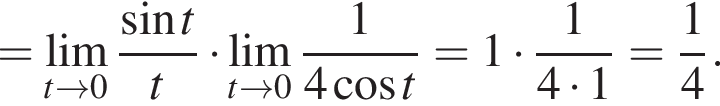
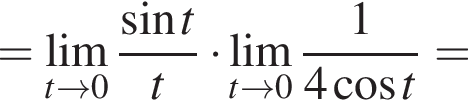
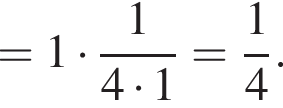
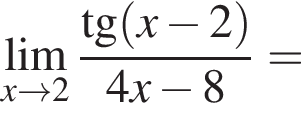
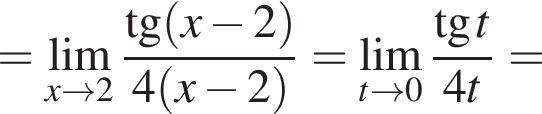
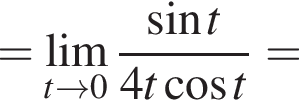
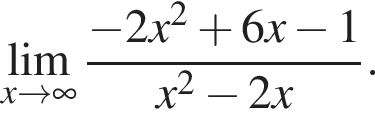
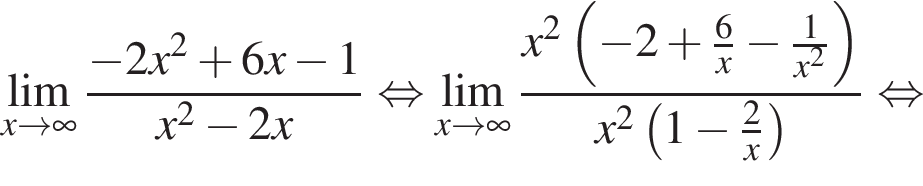
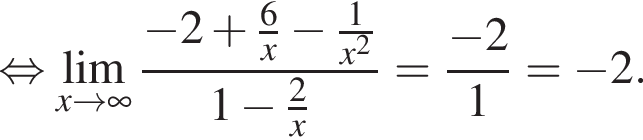
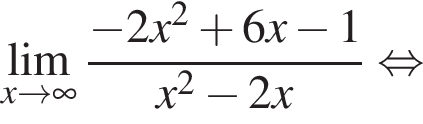
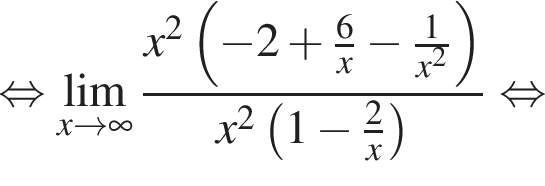
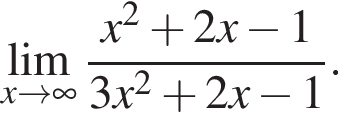
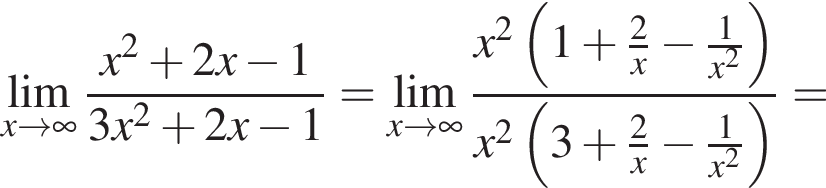
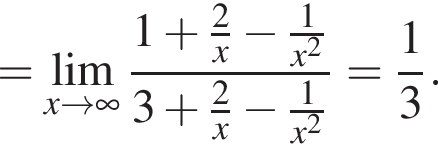
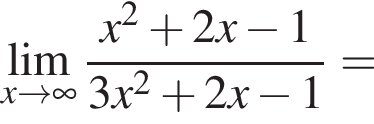
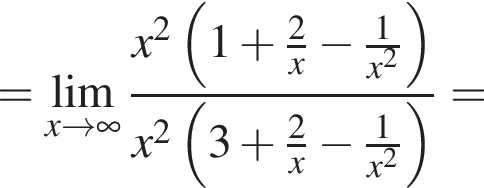
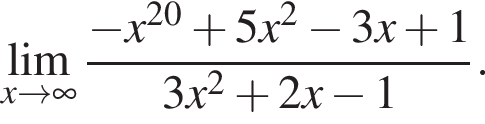
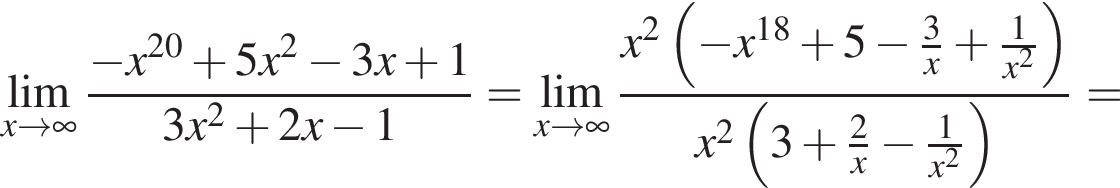
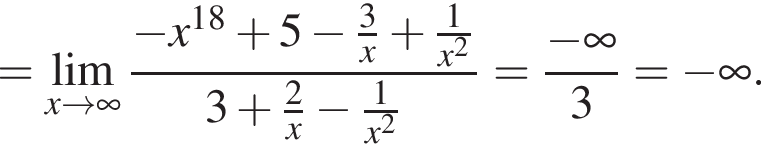
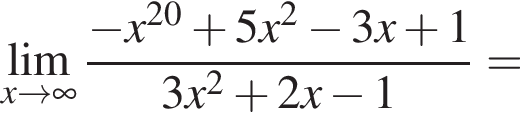
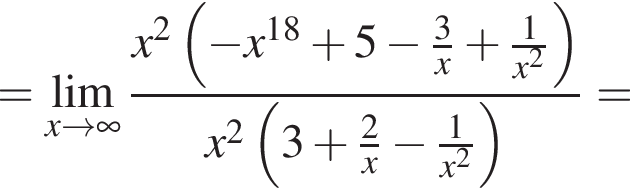
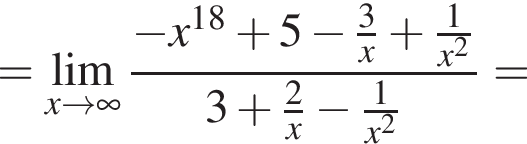
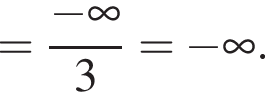
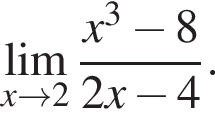
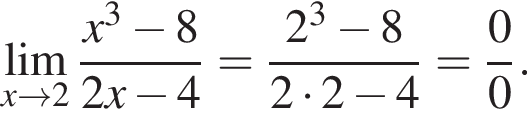
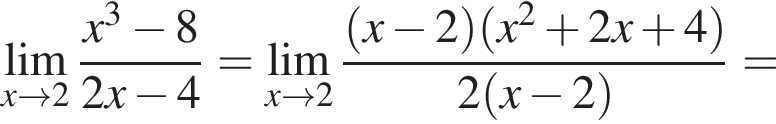

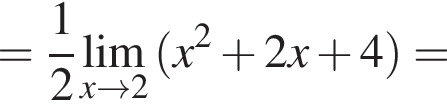
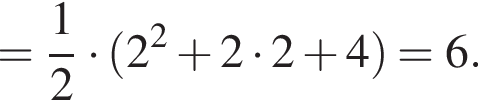
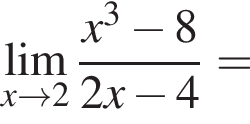
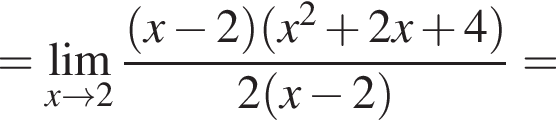
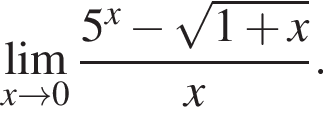
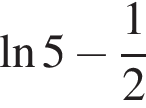
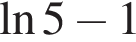
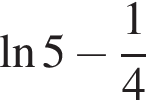
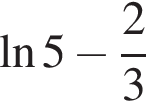
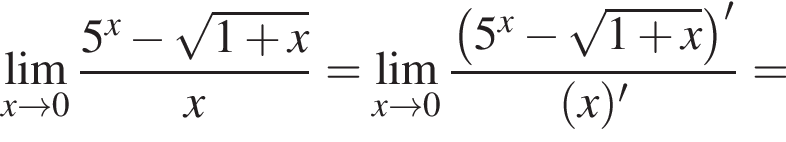
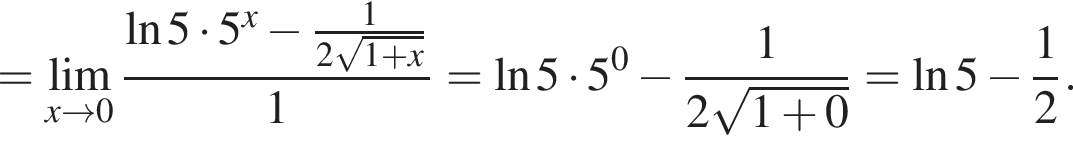
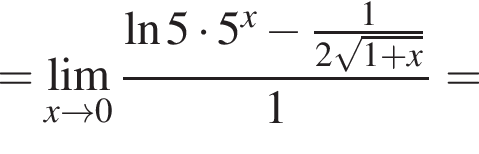
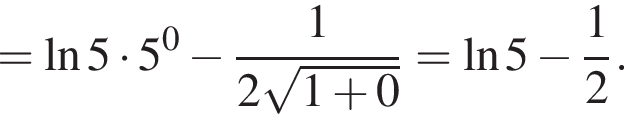
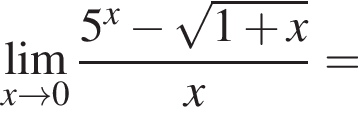

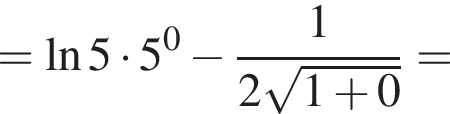
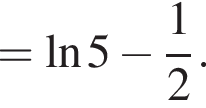
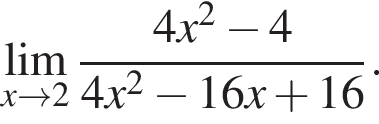
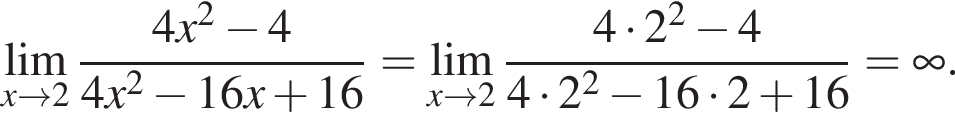
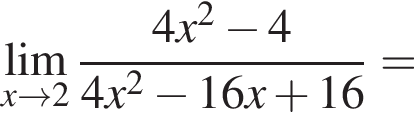
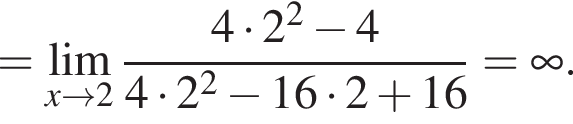
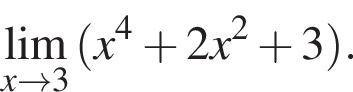
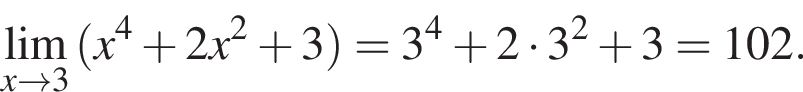
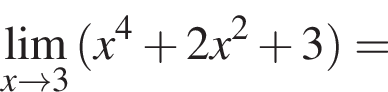

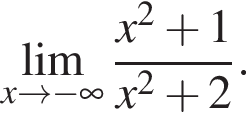
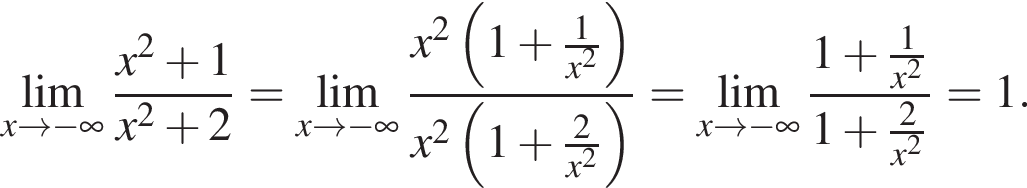
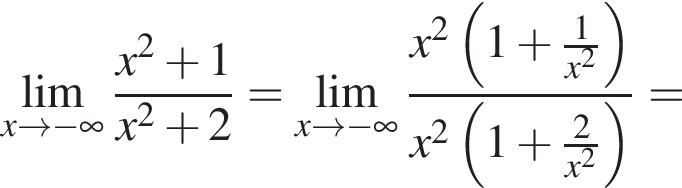
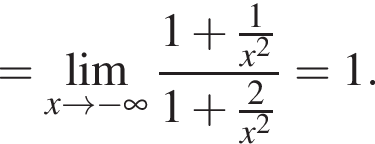
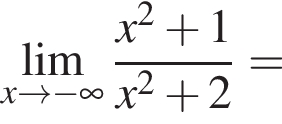
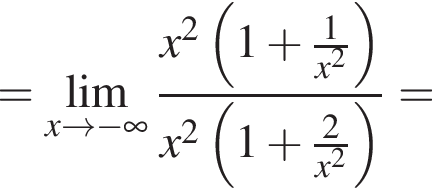
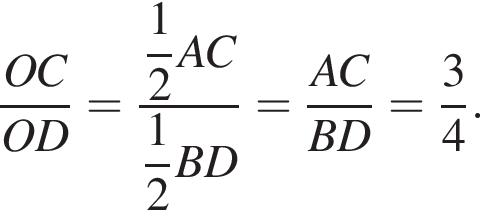
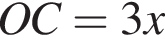 и
и  тогда по теореме Пифагора для треугольника OCD получаем
тогда по теореме Пифагора для треугольника OCD получаем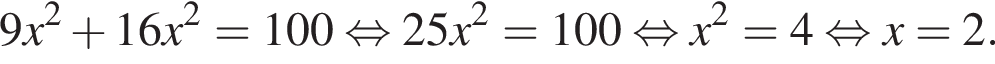

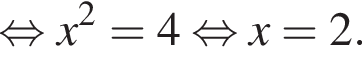


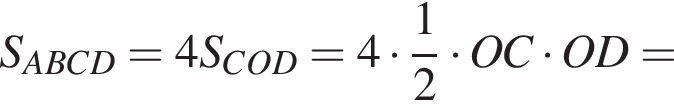
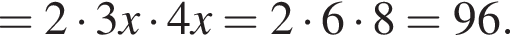

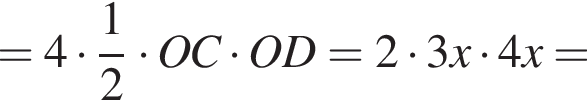
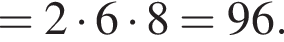
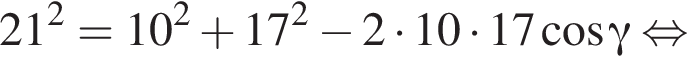

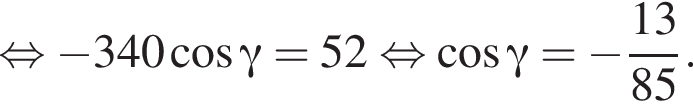

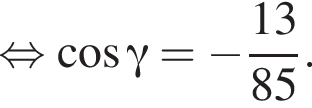

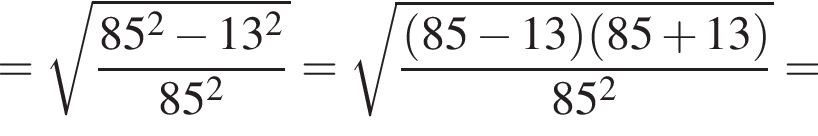
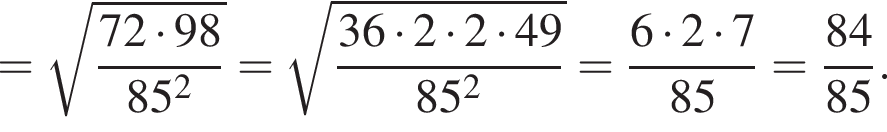
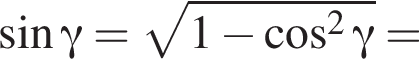
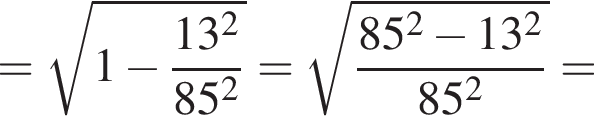
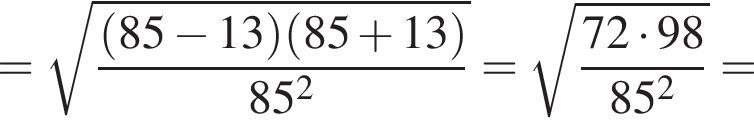
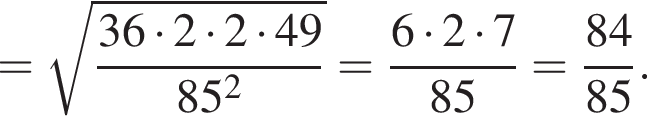
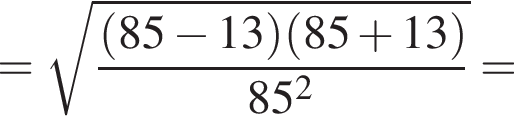
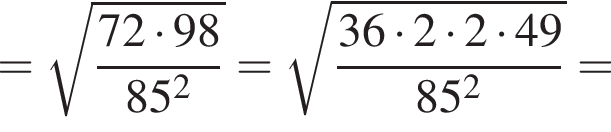
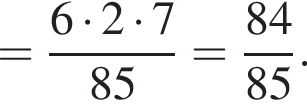
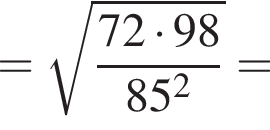


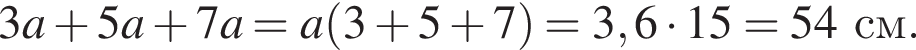

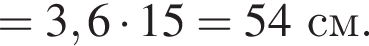

 способами.
способами.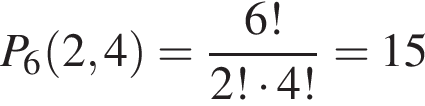 способами.
способами.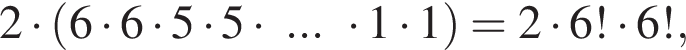 поскольку мальчики могут сидеть либо справа, либо слева от девочек.
поскольку мальчики могут сидеть либо справа, либо слева от девочек. (касательная перпендикулярна радиусу) и
(касательная перпендикулярна радиусу) и 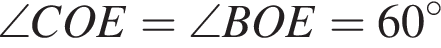 (как угол равностороннего треугольника). Значит,
(как угол равностороннего треугольника). Значит,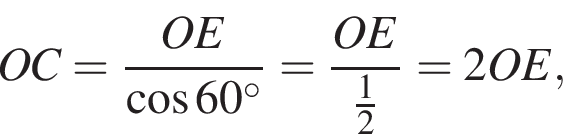




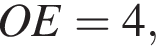
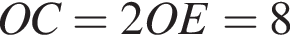 и по теореме Пифагора
и по теореме Пифагора 
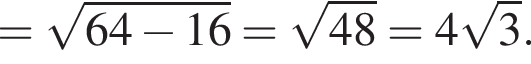
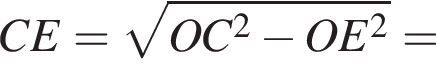

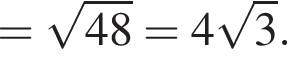

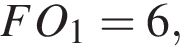
 Радиус второй окружности равен
Радиус второй окружности равен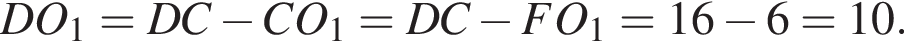
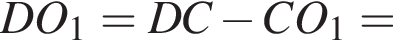

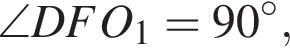 так как касательная перпендикулярна радиусу, поэтому
так как касательная перпендикулярна радиусу, поэтому 
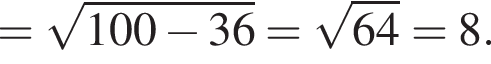
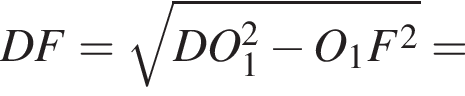
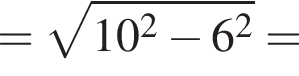
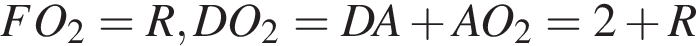
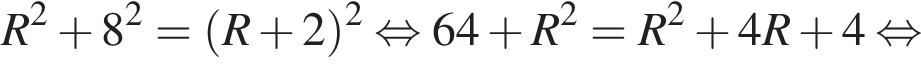
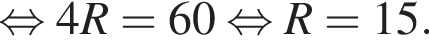
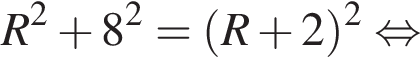

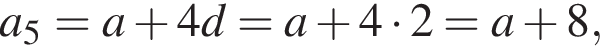

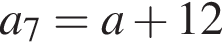 и
и 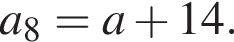 По условию
По условию 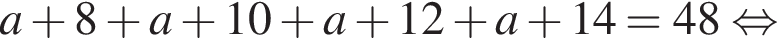

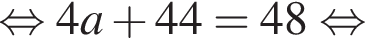
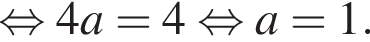
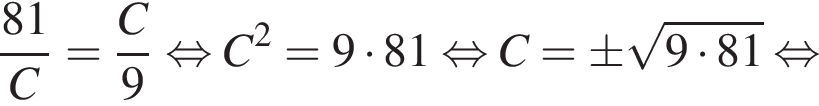
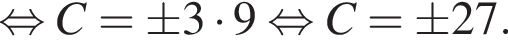
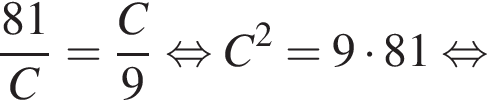

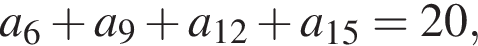 то S20 равна?
то S20 равна?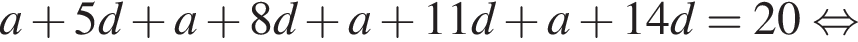
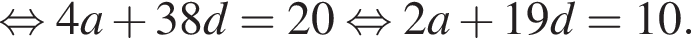
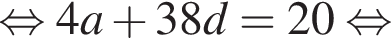
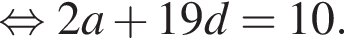


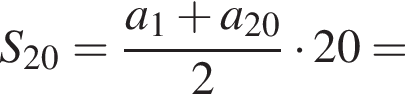
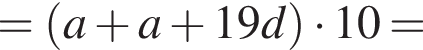
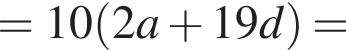
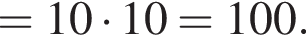
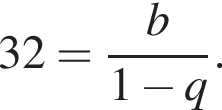
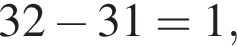 при этом они тоже образуют бесконечно убывающую геометрическую прогрессию. Значит,
при этом они тоже образуют бесконечно убывающую геометрическую прогрессию. Значит, 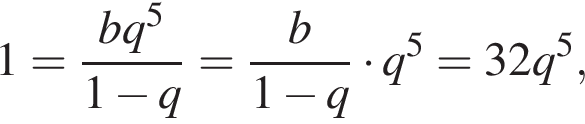
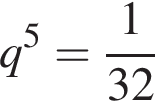 и
и 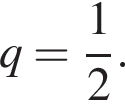 Тогда
Тогда 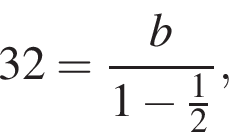 поэтому
поэтому  откуда
откуда 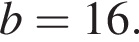
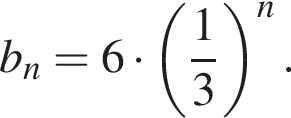
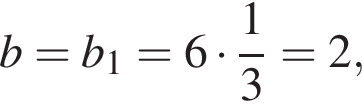 знаменатель прогрессии очевидно равен
знаменатель прогрессии очевидно равен 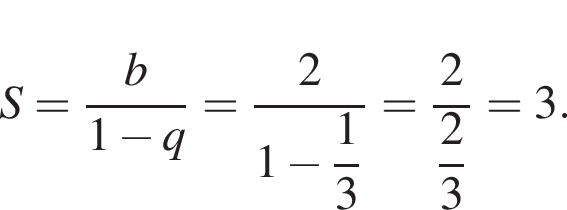
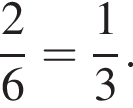 По формуле суммы бесконечно убывающей геометрической прогрессии получаем
По формуле суммы бесконечно убывающей геометрической прогрессии получаем 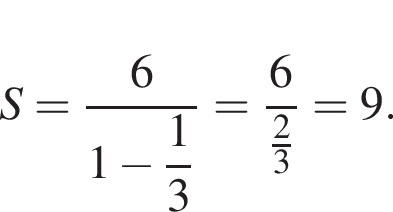
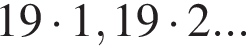 Выпишем эти числа до 149 и сразу прибавим единицу. Получим числа 20, 39, 58, 77, 96, 115, 134, 153 (а число 172 уже слишком велико). Сумма этих восьми чисел составляет
Выпишем эти числа до 149 и сразу прибавим единицу. Получим числа 20, 39, 58, 77, 96, 115, 134, 153 (а число 172 уже слишком велико). Сумма этих восьми чисел составляет 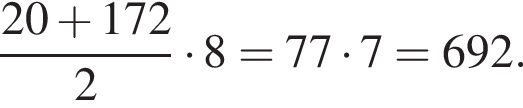
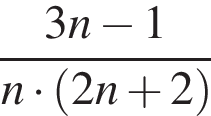
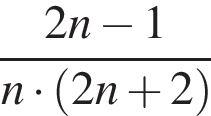
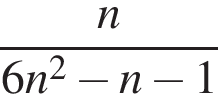
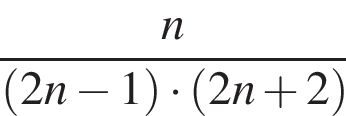
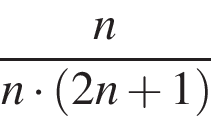
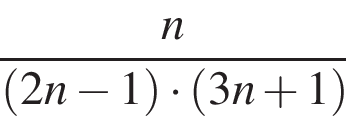
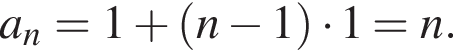
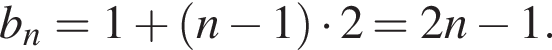
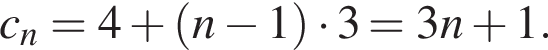
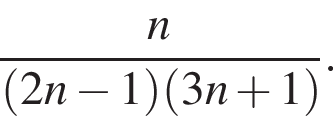
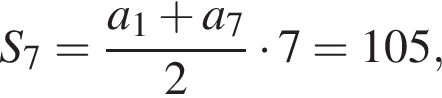 откуда
откуда 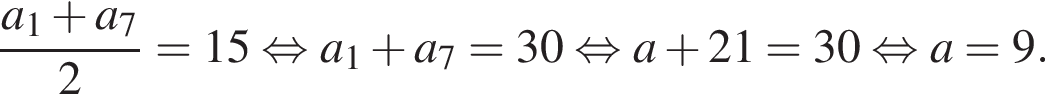
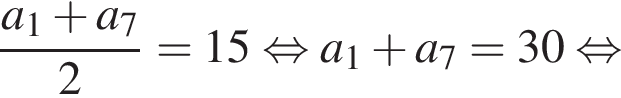
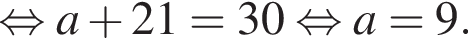
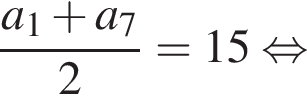
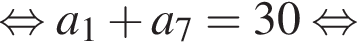
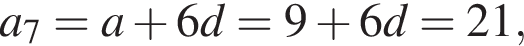 откуда
откуда  и
и 
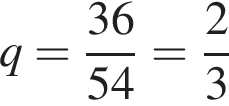 как отношение соседних членов геометрической прогрессии.
как отношение соседних членов геометрической прогрессии.