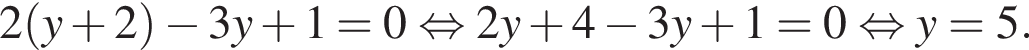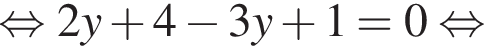1. Тип Д36 A36 № 2052 

Источник: Демонстрационная версия ЕНТ по математике 2022 года, вариант 1. Отредактировано редакцией Решу ЕНТ в формат актуальной демоверсии
Классификатор алгебры: 1\.12\. Вычисления и преобразования с модулем
Простые вопросы о числах, НОД и НОК, делители, доли, проценты. Задания для подготовки
i
Bыберите верные равенства:
1. 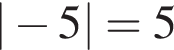
2. 
3. ![]()
4. 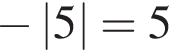
1) 3 и 4
2) 1 и 2
3) 2 и 4
4) 1 и 3
Решение. Заметим, что 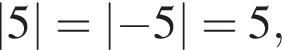 поэтому верны первое и третье равенства.
поэтому верны первое и третье равенства.
Правильный ответ указан под номером 4.
Ответ: 4
2052
4
Источник: Демонстрационная версия ЕНТ по математике 2022 года, вариант 1. Отредактировано редакцией Решу ЕНТ в формат актуальной демоверсии
Классификатор алгебры: 1\.12\. Вычисления и преобразования с модулем
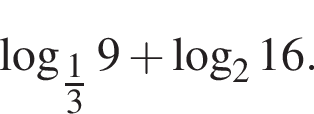
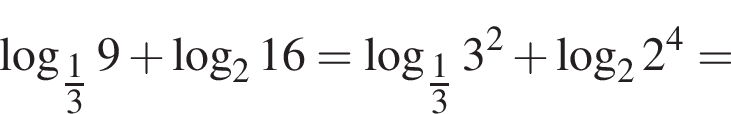
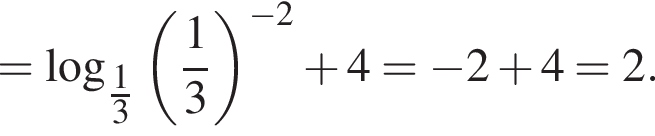
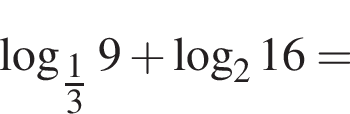
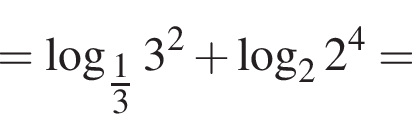
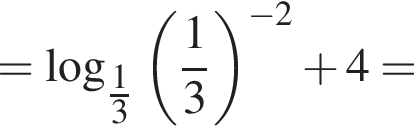

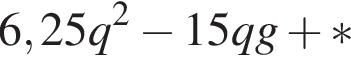 можно было представить в виде квадрата двучлена
можно было представить в виде квадрата двучлена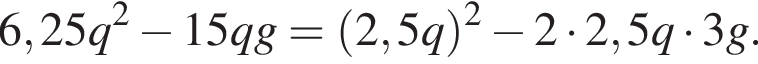
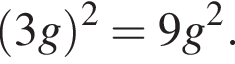
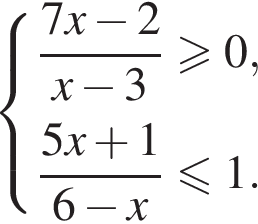

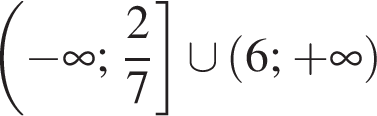
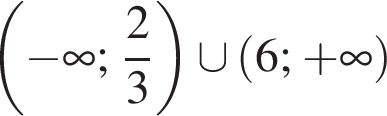
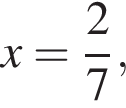 корнем знаменателя
корнем знаменателя 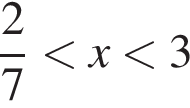 числитель положителен, а знаменатель отрицателен (такие x не подходят), при
числитель положителен, а знаменатель отрицателен (такие x не подходят), при 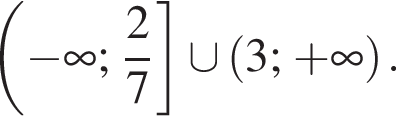
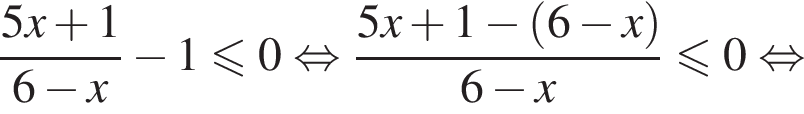
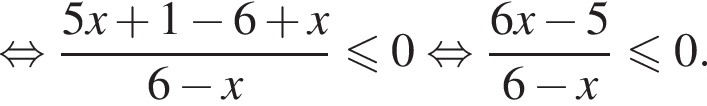
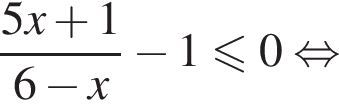
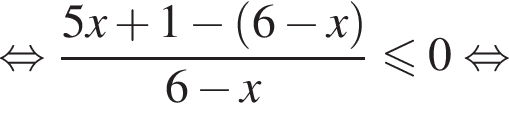
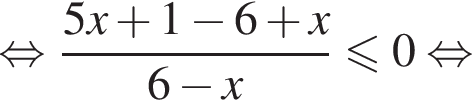
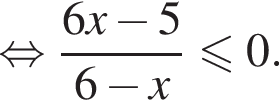
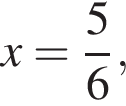 корнем знаменателя
корнем знаменателя 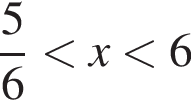 числитель и знаменатель положительны (такие x не подходят), при
числитель и знаменатель положительны (такие x не подходят), при 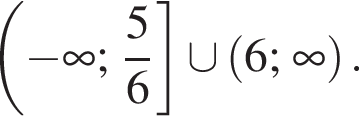
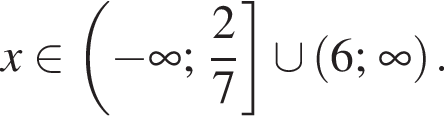
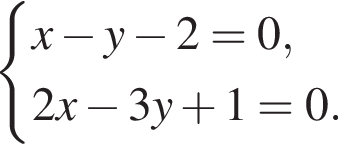
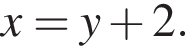 Подставляя это выражение во второе уравнение, получаем
Подставляя это выражение во второе уравнение, получаем