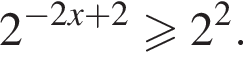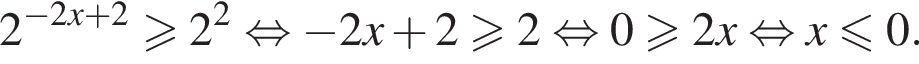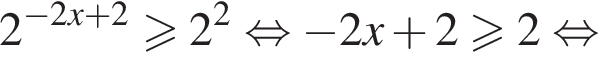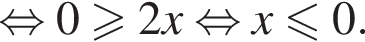Корнями уравнения 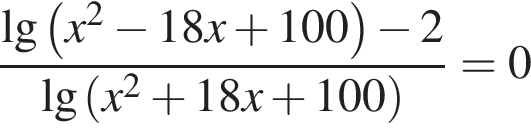 являются?
являются?
1) −10
2) 10
3) −18
4) 9
5) 18
6) 0
7) 2
8) 1
Решение. Решим сначала уравнение

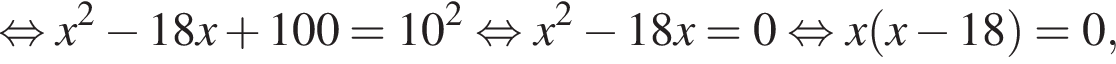
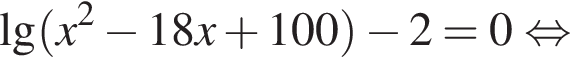


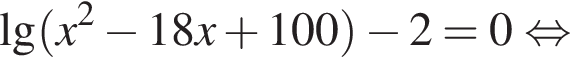
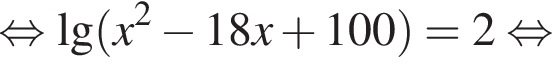
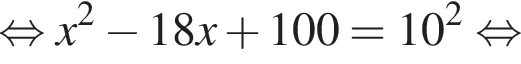

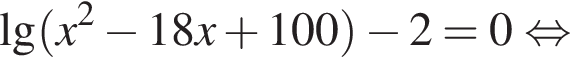
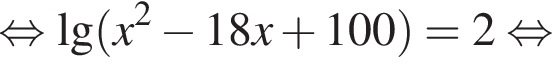
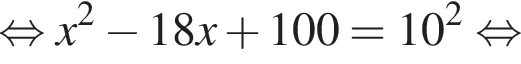
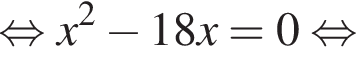
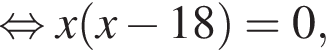
откуда ![]() или
или 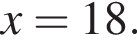 Ясно что для обоих этих корней знаменатель определен и не равен нулю, поэтому они действительно корни исходного уравнения.
Ясно что для обоих этих корней знаменатель определен и не равен нулю, поэтому они действительно корни исходного уравнения.
Правильные ответы указаны под номерами 5 и 6.
Ответ: 56
37
56
Источники:

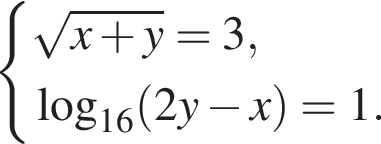
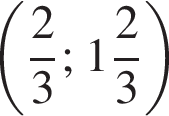

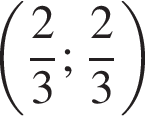
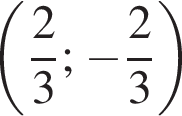
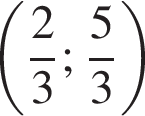
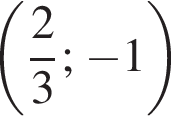
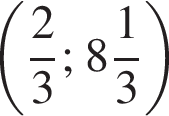
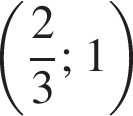
 а второе
а второе 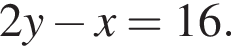 Складывая эти уравнения, получим
Складывая эти уравнения, получим  откуда
откуда 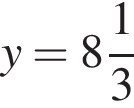 и
и 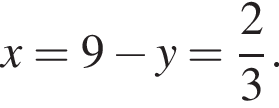 Эти числа даны в ответах 2 и 7, просто по-разному записаны.
Эти числа даны в ответах 2 и 7, просто по-разному записаны. 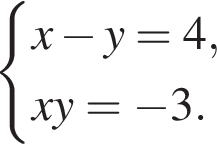
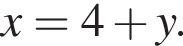 Подставляя это выражение во второе уравнение, получим
Подставляя это выражение во второе уравнение, получим 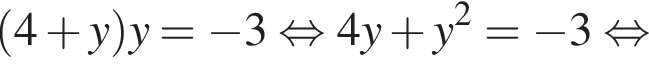

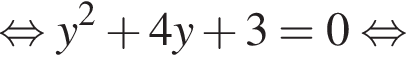
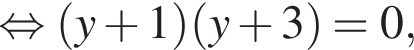
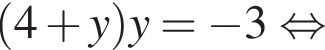

 и
и 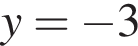 и
и 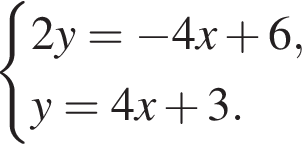
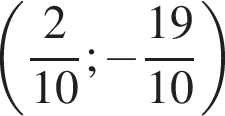

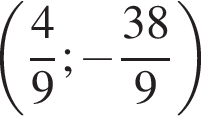
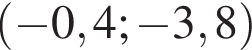
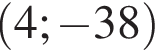

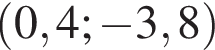
 откуда
откуда 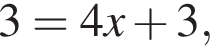 откуда
откуда 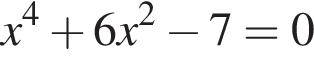 являются?
являются?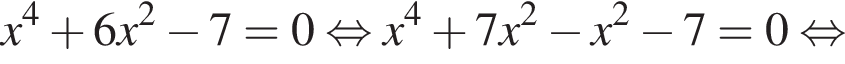
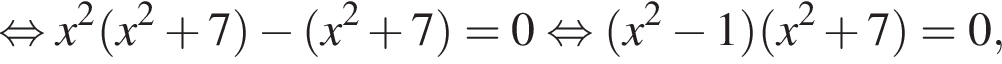
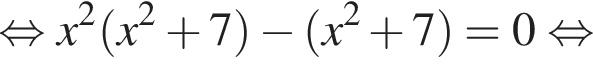
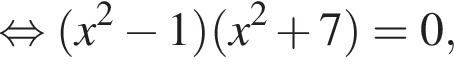

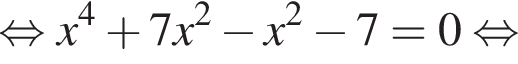
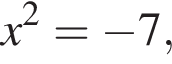 что невозможно, либо
что невозможно, либо  откуда
откуда 
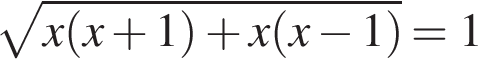 являются
являются
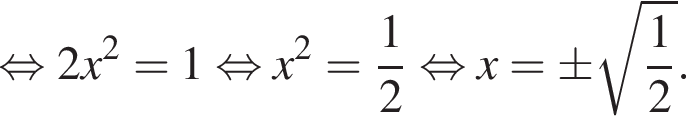
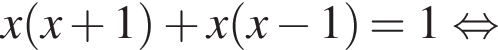
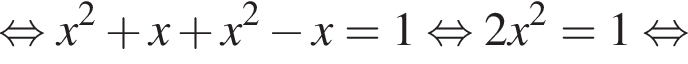
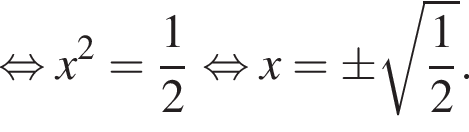
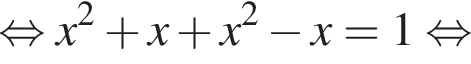
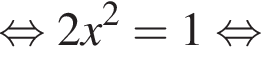
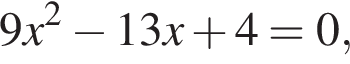 то среди предложенных чисел найдите
то среди предложенных чисел найдите  и
и 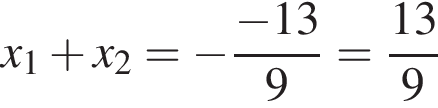 и
и  находим
находим 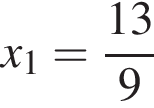 или
или 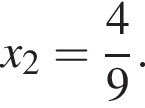 Эти числа даны в ответах 4 и 7.
Эти числа даны в ответах 4 и 7.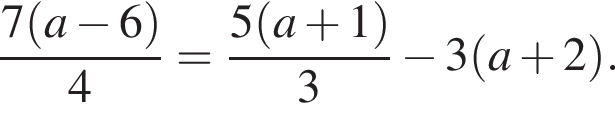
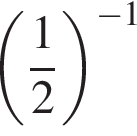
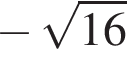
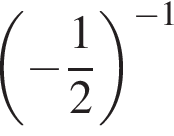
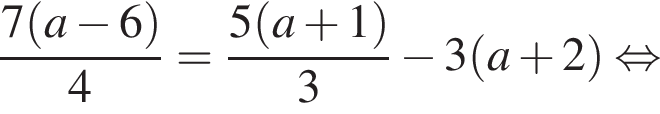

 являются?
являются?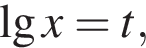 тогда
тогда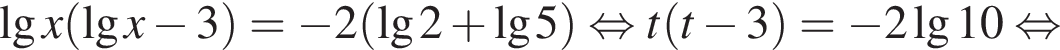

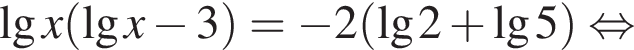


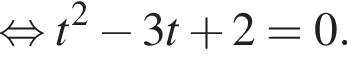
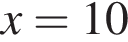 или
или  Эти числа даны в ответах 5 и 7.
Эти числа даны в ответах 5 и 7.


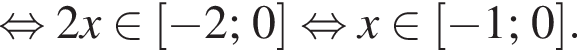
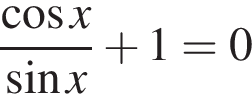 при
при 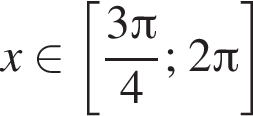 являются?
являются? откуда его корни это
откуда его корни это 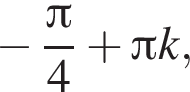
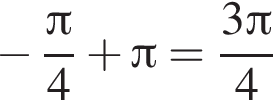 и
и 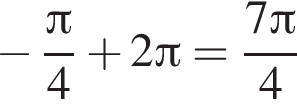
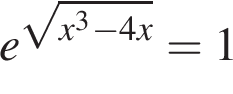 являются?
являются?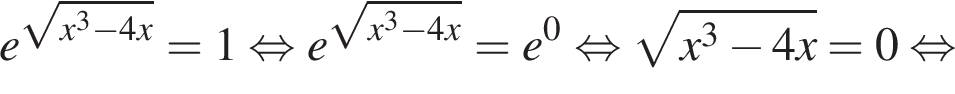
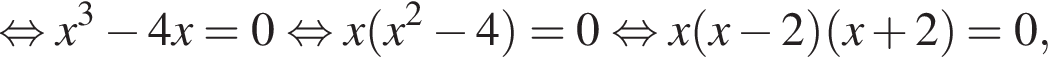
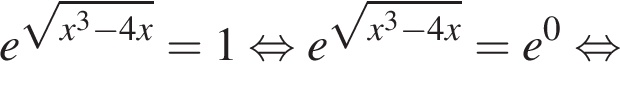

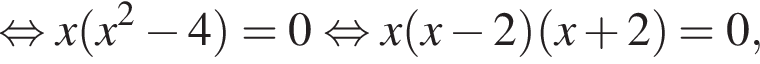
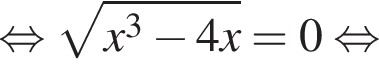

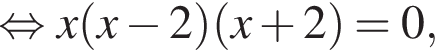
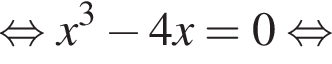
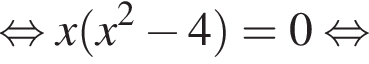
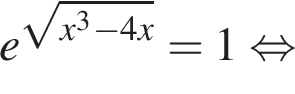
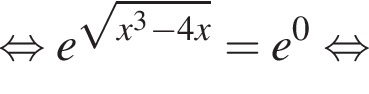

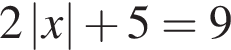 являются?
являются?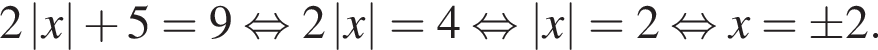

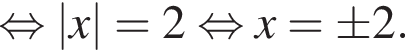
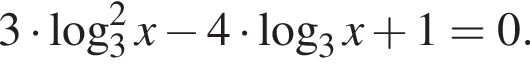
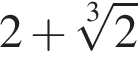
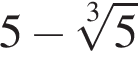
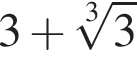
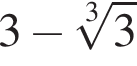
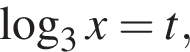 тогда
тогда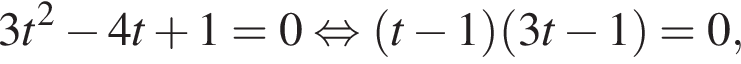
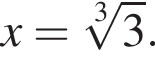 Значит, ответом будет номер 5.
Значит, ответом будет номер 5.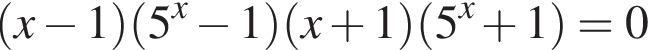 являются
являются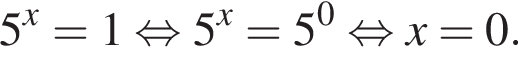
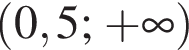

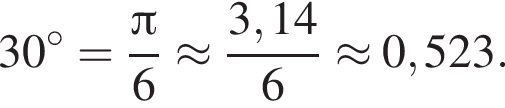
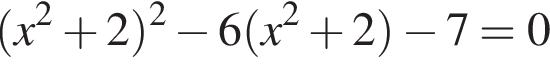 являются?
являются?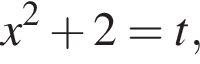 тогда уравнение примет вид
тогда уравнение примет вид 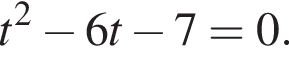 Решая это квадратное уравнение, получим
Решая это квадратное уравнение, получим  или
или 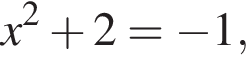 откуда
откуда 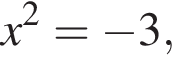 что невозможно. Либо
что невозможно. Либо 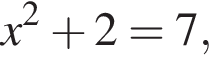 откуда
откуда  то есть
то есть 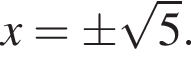 Подходят ответы 3 и 6.
Подходят ответы 3 и 6. 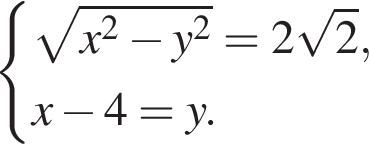
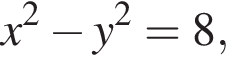 то есть
то есть 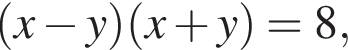 при этом из второго уравнения следует, что
при этом из второго уравнения следует, что  Значит,
Значит, 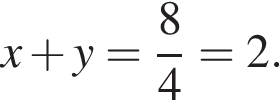 В принципе можно было бы здесь остановиться, но на всякий случай дорешаем систему. Складывая уравнения
В принципе можно было бы здесь остановиться, но на всякий случай дорешаем систему. Складывая уравнения 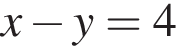 и
и  находим
находим  то есть
то есть 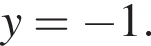 Для этих чисел
Для этих чисел 
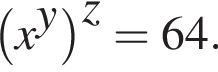
 причем
причем  Это позволяет подставить все наборы и установить, какие из них годятся.
Это позволяет подставить все наборы и установить, какие из них годятся.